
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,建立直角坐标系.
轴,建立直角坐标系.

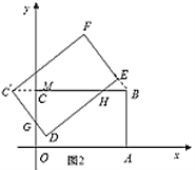
(Ⅰ)将矩形![]() 绕点
绕点![]() 逆时针旋转至矩形
逆时针旋转至矩形![]() ,如图1,
,如图1,![]() 经过点
经过点![]() ,求旋转角的大小和点
,求旋转角的大小和点![]() ,
,![]() 的坐标;
的坐标;
(Ⅱ)将图1中矩形![]() 沿直线
沿直线![]() 向左平移,如图2,平移速度是每秒1个单位长度.
向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线![]() 经过点
经过点![]() ;
;
②设两矩形重叠部分的面积为![]() ,运动时间为
,运动时间为![]() ,写出重叠部分面积
,写出重叠部分面积![]() 与时间
与时间![]() 之间的函数关系式.
之间的函数关系式.
【答案】(Ⅰ)旋转角![]() ;
;![]() ,
,![]() ;(Ⅱ)①
;(Ⅱ)①![]() ;②
;②![]() (
(![]() ),
),![]() (
(![]() ).
).
【解析】
(Ⅰ)根据OA=4,OC=2,BC=OA,可求得BC=2CD,则可以求出∠BCD=60°,即可求出旋转角∠OCD的度数;作DM⊥CB于点M,FN⊥CB于点N,在Rt△CDM中,根据三角函数即可求得DM,CM的长,从而求得D的坐标,在Rt△CFN中,根据三角函数即可求得CN,FN的长,即得F的坐标;(Ⅱ)①如图2,HB即为直线EF经过点B时移动的距离.在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在△HEB中,利用三角函数求得BH,即可求得时间.
②先根据三角函数求出C′H的长,重合的部分可能是四边形,也可能是三角形,分两种情况进行讨,分别原t表示出CC′、CG、CH和C′G的长,利用面积公式即可得S与t的关系式.
(Ⅰ)如图1,在矩形![]() 中,OA=4,
中,OA=4,![]() ,
,

∴在![]() 中,
中,![]() ,即
,即![]()
∴旋转角![]() .
.
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴点![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴点![]() 到
到![]() 轴的距离为4.
轴的距离为4.
故![]() ,
,![]() .
.
(Ⅱ)①如图2,![]() 即为直线
即为直线![]() 经过点
经过点![]() 时移动的距离.
时移动的距离.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,则
,则![]() .
.
∵平移速度是每秒1个单位长度,
∴直线![]() 经过点
经过点![]() 时所需的时间
时所需的时间![]() 秒.
秒.
②过点![]() 作
作![]() 于点
于点![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
当![]() 时,重叠部分面积为四边形
时,重叠部分面积为四边形![]() ,如图2.
,如图2.
![]() ,
,![]() ,
,![]() .
.
当![]() 时,重叠部分的面积为
时,重叠部分的面积为![]() ,如图3.
,如图3.
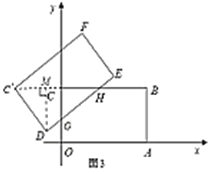
![]() ,
,![]() ,
,![]() .
.
∴重叠部分的面积![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
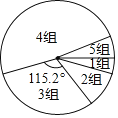
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() ,且
,且![]() ,点
,点![]() 在射线
在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且满足
重合),且满足![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .设
.设![]()
![]() .
.
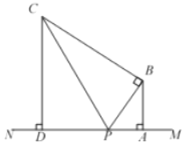
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)①线段![]() 的长是________;
的长是________;
②线段![]() 的长是_________;(用含
的长是_________;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 为何值时,
为何值时,![]() 有最小值?并求出这个最小值.
有最小值?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知抛物线y= x2 -2px+q.
(1)当p=2 时,
①抛物线的顶点坐标横坐标为____ ___,纵坐标为__________(用含 q 的式子表示);
②若点 A(-1,y1),B(x2,y2 )都在抛物线上,且y2 >y1,令x2 = m,则 m的取值范围是_____________;
(2)已知点 M(3,2),将点 M 向左平移 5 个单位长度,得到点 N.当q=6 时,若抛物线与线段 MN 恰有一个公共点,结合函数图象,求 p 的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组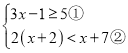
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com