
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
【答案】(1)y=-x![]() +30x-200;(2)在0<x<15元时,每天的销售利润随着x的增大而增大
+30x-200;(2)在0<x<15元时,每天的销售利润随着x的增大而增大
【解析】
(1)直接利用待定系数法求出一次函数解析式进而得出销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)直接得出二次函数对称轴进而利用二次函数增减性得出答案.
解:(1)由图象,设一次函数解析式为:m=kx+b,
将(0,20),(20,0)代入得:![]() ,
,
解得:![]() 求得一次函数的解析式为:m=-x+20
求得一次函数的解析式为:m=-x+20
每件商品的利润为x-10,所以每天的利润为:
y=(x-10)(-x+20)
∴函数解析式为y=-x![]() +30x-200
+30x-200
(2)∵x=-![]() =15(元)
=15(元)
在0<x<15元时,每天的销售利润随着x的增大而增大.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
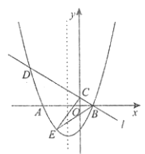
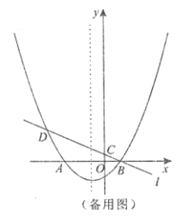
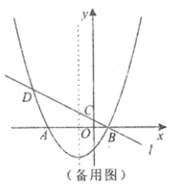
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() .
.
(1)则点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,抛物线的对称轴为__________;
的坐标为__________,抛物线的对称轴为__________;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,当
下方抛物线上的一点,当![]() 时.求
时.求![]() 面积的最大值;
面积的最大值;
(3)设![]() 为抛物线对称轴上一点,点
为抛物线对称轴上一点,点![]() 在抛物线上,若以点
在抛物线上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形,求
为顶点的四边形为矩形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,建立直角坐标系.
轴,建立直角坐标系.

(Ⅰ)将矩形![]() 绕点
绕点![]() 逆时针旋转至矩形
逆时针旋转至矩形![]() ,如图1,
,如图1,![]() 经过点
经过点![]() ,求旋转角的大小和点
,求旋转角的大小和点![]() ,
,![]() 的坐标;
的坐标;
(Ⅱ)将图1中矩形![]() 沿直线
沿直线![]() 向左平移,如图2,平移速度是每秒1个单位长度.
向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线![]() 经过点
经过点![]() ;
;
②设两矩形重叠部分的面积为![]() ,运动时间为
,运动时间为![]() ,写出重叠部分面积
,写出重叠部分面积![]() 与时间
与时间![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
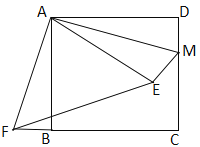
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
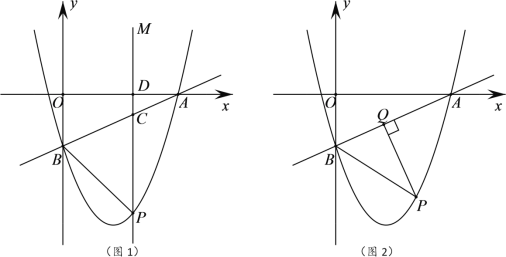
(1)求此抛物线对应的函数表达式;
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com