
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
【答案】(1)14元/千克;(2)5月下旬售价确定为16元/![]() 时,每天获得毛利最大,最大毛利2450元.
时,每天获得毛利最大,最大毛利2450元.
【解析】
(1)设售价降价x元,根据每天的毛利=每千克的毛利×销售量,列出方程,解出x值即可.
(2)①设单价涨价![]() 元时,每天的毛利为
元时,每天的毛利为![]() 元,根据每天的毛利=每千克的毛利
元,根据每天的毛利=每千克的毛利![]() 销售量,列出关系式,根据二次函数的性质,即可求出最值;②设单价降价
销售量,列出关系式,根据二次函数的性质,即可求出最值;②设单价降价![]() 元时,每天的毛利为
元时,每天的毛利为![]() 元,同①可得;然后①②比较即得结论.
元,同①可得;然后①②比较即得结论.
(1)解:要兼顾顾客利益,应考虑降价模式.设售价降价x元,则
![]()
约简,得![]() .
.
整理,得![]() .
.
∴![]() .
.
即5月中旬确定售价为![]() (元
(元![]() );
);
(2)解:①设单价涨价![]() 元时,每天的毛利为
元时,每天的毛利为![]() 元,则
元,则
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() 最大为2450元.
最大为2450元.
∴售价确定为![]() 元/
元/![]() 时,专卖店每天获得最大毛利2450元.
时,专卖店每天获得最大毛利2450元.
②设单价降价![]() 元时,每天的毛利为
元时,每天的毛利为![]() 元,则
元,则
![]()
![]()
![]()
![]() .
.
当![]() 时,
时,![]() 最大为2400元.
最大为2400元.
即售价为![]() 元/
元/![]() 时,专卖店每天获得最大毛利2400元.
时,专卖店每天获得最大毛利2400元.
比较可知,5月下旬售价确定为16元/![]() 时,每天获得毛利最大,最大毛利2450元.
时,每天获得毛利最大,最大毛利2450元.
故答案为:(1)14元/千克;(2)5月下旬售价确定为16元/![]() 时,每天获得毛利最大,最大毛利2450元.
时,每天获得毛利最大,最大毛利2450元.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
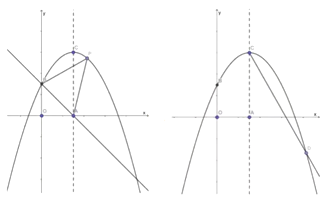
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组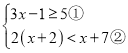
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以矩形![]() 的顶点
的顶点![]() 为坐标原点建立平面直角坐标系,使点
为坐标原点建立平面直角坐标系,使点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,双曲线
轴的正半轴上,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,过
,过![]() 边上一点
边上一点![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在矩形内部的一点
落在矩形内部的一点![]() 处,且
处,且![]() ,若点
,若点![]() 的坐标为(2,4),则
的坐标为(2,4),则![]() 的值为______.
的值为______.
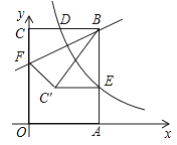
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°和106°,由此可知三角板的较短直角边的长度为 cm.(参考数据:tan37°=0.75)
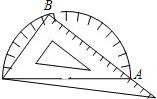
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com