
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
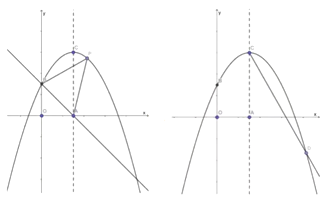
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 最大值为
最大值为![]() ;(3)存在,
;(3)存在,![]() 点坐标为
点坐标为![]() ,理由见解析
,理由见解析
【解析】
(1)利用待定系数法可求出二次函数的解析式;
(2)求三角形面积的最值,先求出三角形面积的函数式.从图形上看S△PAB=S△BPO+S△APO-S△AOB,设P![]() 求出关于n的函数式,从而求S△PAB的最大值.
求出关于n的函数式,从而求S△PAB的最大值.
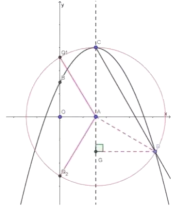
(3) 求点D的坐标,设D![]() ,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点
,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点![]() ,使
,使![]() ?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
解:![]() 抛物线顶点为
抛物线顶点为![]()
![]() 可设抛物线解析式为
可设抛物线解析式为![]()
将![]() 代入
代入![]() 得
得
![]()
![]()
![]() 抛物线
抛物线![]() ,即
,即![]()
![]() 连接
连接![]() ,
,
![]()
设![]() 点坐标为
点坐标为![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最大值为
最大值为![]()

![]() 存在,设点D的坐标为
存在,设点D的坐标为![]()
过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,
,
则![]()
![]()
![]()
在![]() 中有
中有
![]()
![]()
化简得![]()
![]() (舍去),
(舍去),![]()
∴点D(![]() ,-3)
,-3)
![]()
连接![]() ,在
,在![]() 中
中
![]()
![]()
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 轴的交点上
轴的交点上
此时![]()
设![]() 点为(0,m), AQ为
点为(0,m), AQ为![]() 的半径
的半径
则AQ=OQ+OA, 6=m+3
即![]()
∴![]()
综上所述,![]() 点坐标为
点坐标为![]()
故存在点Q,且这样的点有两个点.


科目:初中数学 来源: 题型:
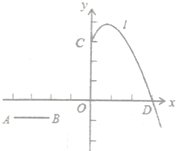
【题目】已知:如图,点![]() ,
,![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]()
(1)当![]() 时,求该抛物线与
时,求该抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)当![]() 时,求
时,求![]() 的最大值(用含
的最大值(用含![]() 的代数式表示);
的代数式表示);
(3)当抛物线![]() 经过点
经过点![]() 时,
时,![]() 的解析式为__________,顶点坐标为__________,点
的解析式为__________,顶点坐标为__________,点![]() __________(填“是”或“否”)在
__________(填“是”或“否”)在![]() 上.
上.
若线段![]() 以每秒2个单位长的速度向下平移,设平移的时间为
以每秒2个单位长的速度向下平移,设平移的时间为![]() (秒).
(秒).
①若![]() 与线段
与线段![]() 总有公共点,求
总有公共点,求![]() 的取值范围;
的取值范围;
②若![]() 同时以每秒3个单位长的速度向下平移,
同时以每秒3个单位长的速度向下平移,![]() 在
在![]() 轴及其右侧的图象与直线
轴及其右侧的图象与直线![]() 总有两个公共点,直接写出
总有两个公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
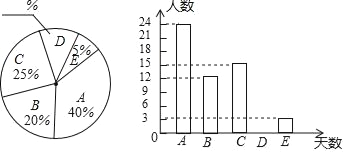
请根据以上的信息,回答下列问题:
(1)补全扇形统计图和条形统计图;
(2)所抽查学生参加社会实践活动天数的众数是 (选填:A、B、C、D、E);
(3)若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在数学课上带领同学们做数学游戏,规则如下:
游戏规则
甲任报一个有理数数传给乙;
乙把这个数减![]() 后报给丙;
后报给丙;
丙再把所得的数的绝对值报给丁;
丁再把这个数的一半减![]() ,报出答案.
,报出答案.
根据游戏规则,回答下面的问题:
(1)若甲报的数为![]() ,则乙报的数为_________,丁报出的答案是_________;
,则乙报的数为_________,丁报出的答案是_________;
(2)若甲报的数为![]() ,请列出算式并计算丁报出的答案;
,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是![]() ,则直接写出甲报的数.
,则直接写出甲报的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com