
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() гы
гы![]() жсЦНааЃЌЧв
жсЦНааЃЌЧв![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓИУХзЮяЯпгы
ЪБЃЌЧѓИУХзЮяЯпгы![]() жсЕФНЛЕузјБъЃЛ
жсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФзюДѓжЕЃЈгУКЌ
ЕФзюДѓжЕЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉЕБХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЌ
ЪБЃЌ![]() ЕФНтЮіЪНЮЊ__________ЃЌЖЅЕузјБъЮЊ__________ЃЌЕу
ЕФНтЮіЪНЮЊ__________ЃЌЖЅЕузјБъЮЊ__________ЃЌЕу![]() __________ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉдк
__________ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉдк![]() ЩЯЃЎ
ЩЯЃЎ
ШєЯпЖЮ![]() вдУПУы2ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌЩшЦНвЦЕФЪБМфЮЊ
вдУПУы2ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌЩшЦНвЦЕФЪБМфЮЊ![]() ЃЈУыЃЉЃЎ
ЃЈУыЃЉЃЎ
ЂйШє![]() гыЯпЖЮ
гыЯпЖЮ![]() змгаЙЋЙВЕуЃЌЧѓ
змгаЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
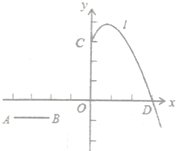
ЂкШє![]() ЭЌЪБвдУПУы3ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌ
ЭЌЪБвдУПУы3ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌ![]() дк
дк![]() жсМАЦфгвВрЕФЭМЯѓгыжБЯп
жсМАЦфгвВрЕФЭМЯѓгыжБЯп![]() змгаСНИіЙЋЙВЕуЃЌжБНгаДГі
змгаСНИіЙЋЙВЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() газюДѓжЕ0ЃЌЕБ
газюДѓжЕ0ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌЗёЃЛЂй
ЃЌЗёЃЛЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБk=1ЪБЃЌИУХзЮяЯпНтЮіЪНy=x2-2x-3ЃЌy=0ЪБЃЌx2-2x-3=0ЃЌНтЕУx1=-1ЃЌx2=3ЃЌИУХзЮяЯпгыxжсЕФНЛЕузјБъЃЈ-1ЃЌ0ЃЉЃЌЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉХзЮяЯпy=kx2-2kx-3kЕФЖдГЦжсжБЯпx=![]() =1ЃЌЕБkЃО0ЪБЃЌx=3ЪБЃЌyгазюДѓжЕЃЌyзюДѓжЕ=9k-6k-3k=0ЃЌЕБkЃМ0ЪБЃЌx=1ЪБЃЌyгазюДѓжЕЃЌyзюДѓжЕ=k-2k-3k=-4kЃЛ
=1ЃЌЕБkЃО0ЪБЃЌx=3ЪБЃЌyгазюДѓжЕЃЌyзюДѓжЕ=9k-6k-3k=0ЃЌЕБkЃМ0ЪБЃЌx=1ЪБЃЌyгазюДѓжЕЃЌyзюДѓжЕ=k-2k-3k=-4kЃЛ
ЃЈ3ЃЉЕБХзЮяЯпОЙ§ЕуCЃЈ0ЃЌ3ЃЉЪБЃЌХзЮяЯпЕФНтЮіЪНЮЊy=-x2+2x+3ЃЌЖЅЕузјБъЃЈ1ЃЌ4ЃЉЃЌAЃЈ-4ЃЌ-1ЃЉЃЌНЋx=-2ДњШыy=-x2+2x+3ЃЌy=-5Ёй-1ЃЌЕуBВЛдкlЩЯЃЛ
ЂйЩшЦНвЦКѓBЃЈ-2ЃЌ-1-2tЃЉЃЌAЃЈ-4ЃЌ-1-2tЃЉЃЌЕБХзЮяЯпОЙ§ЕуBЪБЃЌгаy=-5ЃЌЕБХзЮяЯпОЙ§ЕуAЪБЃЌгаy=-21ЃЌlгыЯпЖЮABзмгаЙЋЙВЕуЃЌдђ-21Ём-1-2tЁм-5ЃЌНтЕУ2ЁмtЁм10ЃЛ
ЂкЦНвЦЙ§ГЬжаЃЌЩшCЃЈ0ЃЌ3-3tЃЉЃЌдђХзЮяЯпЕФЖЅЕуЃЈ1ЃЌ4-3tЃЉЃЌгкЪЧ![]() ЃЌНтЕУ4ЁмtЃМ5ЃЎ
ЃЌНтЕУ4ЁмtЃМ5ЃЎ
НтЃКЃЈ1ЃЉЕБ![]() ЪБЃЌХзЮяЯпНтЮіЪНЮЊ
ЪБЃЌХзЮяЯпНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЫљвдИУХзЮяЯпгы![]() жсЕФНЛЕуЕФзјБъЮЊ
жсЕФНЛЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() газюДѓжЕ0ЃЌ
газюДѓжЕ0ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() ЗёЃЛ
ЗёЃЛ
ЂйЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЕБХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌ
ЃЌ
ЕБХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌ
ЃЌ
ЕБХзЮяЯп![]() гыЯпЖЮ
гыЯпЖЮ![]() змгаЙЋЙВЕуЪБЃЌга
змгаЙЋЙВЕуЪБЃЌга![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
Ђк![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
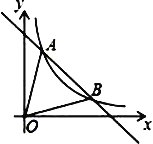
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=Љx+5ЕФЭМЯѓгыЗДБШР§КЏЪ§y=kx-1ЃЈkЁй0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкAЃЈ1ЃЌnЃЉКЭBСНЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНгыЕуBзјБъЃЛ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЕФжБОЖABДЙжБЯвCDгкЕуEЃЌЙ§CЕузїCGЁЮADНЛABбгГЄЯпгкЕуGЃЌСЌНсCOВЂбгГЄНЛADгкЕуFЃЌЧвCFЁЭADЃЎ
ЕФжБОЖABДЙжБЯвCDгкЕуEЃЌЙ§CЕузїCGЁЮADНЛABбгГЄЯпгкЕуGЃЌСЌНсCOВЂбгГЄНЛADгкЕуFЃЌЧвCFЁЭADЃЎ
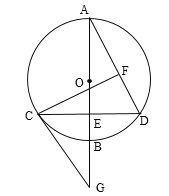
ЃЈ1ЃЉЧѓжЄЃКCGЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=4ЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпyЃНЉx+bНЛyжсгкЕуAЃЌНЛxжсгкЕуBЃЌSЁїAOBЃН![]() ЃЎ
ЃЎ
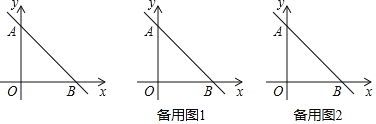
ЃЈ1ЃЉЧѓbЕФжЕЃЛ
ЃЈ2ЃЉЕуCвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгOЕуГіЗЂбиxжсЯђЕуBдЫЖЏЃЌЕуDвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгAЕуГіЗЂбиyжсЯђЕуOдЫЖЏЃЌCЃЌDСНЕуЭЌЪБГіЗЂЃЌЕБЕуDдЫЖЏЕНЕуOЪБЃЌCЃЌDСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎСЌНгCDЃЌЩшЕуCЕФдЫЖЏЪБМфЮЊtУыЃЌЁїCDOЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЬѕМўЯТЃЌЙ§ЕуCзїCEЁЭCDНЛABгкЕуEЃЌЙ§ЕуDзїDFЁЮxжсНЛABгкЕуFЃЌЙ§ЕуFзїFHЁЭCEЃЌДЙзуЮЊHЃЎдкCHЩЯШЁЕуMЃЌЪЙЕУMHЃКHEЃН8ЃК33ЃЌСЌНгFMЃЌШєЁЯFMHЃН![]() ЁЯFEHЃЌЧѓtЕФжЕЃЎ
ЁЯFEHЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§![]() ЕФБпГЄЮЊ2ЃЌЖЅЕу
ЕФБпГЄЮЊ2ЃЌЖЅЕу![]() ЁЂ
ЁЂ![]() дкАыОЖЮЊ
дкАыОЖЮЊ![]() ЕФдВЩЯЃЌЖЅЕу
ЕФдВЩЯЃЌЖЅЕу![]() дкдВФкЃЌНЋе§
дкдВФкЃЌНЋе§![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊЃЌЕБЕу
ФцЪБеыа§зЊЃЌЕБЕу![]() ЕквЛДЮТфдкдВЩЯЪБЃЌдђЕу
ЕквЛДЮТфдкдВЩЯЪБЃЌдђЕу![]() дЫЖЏЕФТЗЯпГЄЮЊ__________ЃЈНсЙћБЃСє
дЫЖЏЕФТЗЯпГЄЮЊ__________ЃЈНсЙћБЃСє![]() ЃЉЃЛШє
ЃЉЃЛШє![]() ЕуТфдкдВЩЯМЧзіЕк1ДЮа§зЊЃЌНЋ
ЕуТфдкдВЩЯМЧзіЕк1ДЮа§зЊЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊЃЌЕБЕу
ФцЪБеыа§зЊЃЌЕБЕу![]() ЕквЛДЮТфдкдВЩЯМЧзіЕк2ДЮа§зЊЃЌдйШЦ
ЕквЛДЮТфдкдВЩЯМЧзіЕк2ДЮа§зЊЃЌдйШЦ![]() НЋ
НЋ![]() ФцЪБеыа§зЊЃЌЕБЕу
ФцЪБеыа§зЊЃЌЕБЕу![]() ЕквЛДЮТфдкдВЩЯЃЌМЧзіЕк3ДЮа§зЊЁЁЃЌШєДЫа§зЊЯТШЅЃЌЕБ
ЕквЛДЮТфдкдВЩЯЃЌМЧзіЕк3ДЮа§зЊЁЁЃЌШєДЫа§зЊЯТШЅЃЌЕБ![]() ЭъГЩЕк2018ДЮа§зЊЪБЃЌ
ЭъГЩЕк2018ДЮа§зЊЪБЃЌ![]() БпЙВЛиЕНдРДЮЛжУ__________ДЮЃЎ
БпЙВЛиЕНдРДЮЛжУ__________ДЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќ![]() жаЃЌ
жаЃЌ![]() Еу
Еу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЖЏЕу(Еу
ЩЯвЛЖЏЕу(Еу![]() ВЛгы
ВЛгы![]() ЁЂ
ЁЂ![]() жиКЯ)ЃЎвд
жиКЯ)ЃЎвд![]() ЮЊБпЯђгвВрзїе§ЗНаЮ
ЮЊБпЯђгвВрзїе§ЗНаЮ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
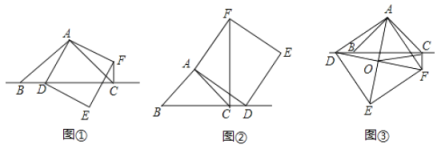
ЃЈВТЯыЃЉШчЭМЂйЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌжБНгаДГі
ЩЯЪБЃЌжБНгаДГі![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЎ
Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЎ
ЃЈЬНОПЃЉШчЭМЂкЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФбгГЄЯпЩЯЪБЃЌХаЖЯ
ЕФбгГЄЯпЩЯЪБЃЌХаЖЯ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
Ш§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈгІгУЃЉШчЭМЂлЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФЗДЯђбгГЄЯпЩЯЪБЃЌЕу
ЕФЗДЯђбгГЄЯпЩЯЪБЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дкжБЯп
ЗжБ№дкжБЯп![]() СНВрЃЌ
СНВрЃЌ![]() ЁЂ
ЁЂ![]() НЛЕуЮЊЕу
НЛЕуЮЊЕу![]() СЌНс
СЌНс![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЁЁЁЁЁЁЁЁЃЎ
ЁЁЁЁЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌODЁЭЯвBCгкЕуFЃЌНЛЁбOгкЕуEЃЌСЌНгCEЃЌAEЃЌCDЃЌШєЁЯAECЃНЁЯODCЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпCDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєABЃН10ЃЌBCЃН8ЃЌдђЯпЖЮCDЕФГЄЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
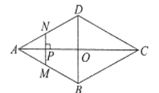
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧСтаЮ
ЪЧСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯвЛЖЏЕуЃЌЙ§
ЩЯвЛЖЏЕуЃЌЙ§![]() зїДЙжБгк
зїДЙжБгк![]() ЕФжБЯпНЛСтаЮ
ЕФжБЯпНЛСтаЮ![]() ЕФБпгк
ЕФБпгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЩш
СНЕуЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() Йигк
Йигк![]() ЕФКЏЪ§ЭМЯѓЕФДѓжТаЮзДЪЧЃЈ ЃЉ
ЕФКЏЪ§ЭМЯѓЕФДѓжТаЮзДЪЧЃЈ ЃЉ
A.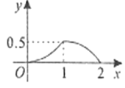 B.
B.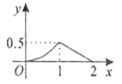
C.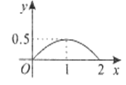 D.
D.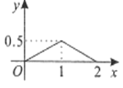
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЕФЖЅЕузјБъЮЊ
ЕФЖЅЕузјБъЮЊ![]() ЃЌВЂгы
ЃЌВЂгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдГЦжсгы
ЪЧЖдГЦжсгы![]() жсЕФНЛЕуЃЎ
жсЕФНЛЕуЃЎ
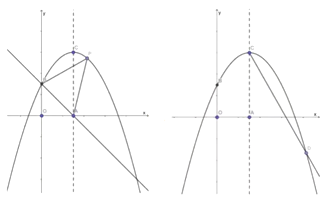
(1)ЧѓХзЮяЯпЕФНтЮіЪН;
(2)ШчЭМЂйЫљЪО, ![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕу,ЧвЮЛгкЕквЛЯѓЯоЃЌСЌНсBPЁЂAP,Чѓ
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕу,ЧвЮЛгкЕквЛЯѓЯоЃЌСЌНсBPЁЂAP,Чѓ![]() ЕФУцЛ§ЕФзюДѓжЕ;
ЕФУцЛ§ЕФзюДѓжЕ;
(3)ШчЭМЂкЫљЪОЃЌдкЖдГЦжс![]() ЕФгвВрзї
ЕФгвВрзї![]() НЛХзЮяЯпгкЕу
НЛХзЮяЯпгкЕу![]() ,ЧѓГі
,ЧѓГі![]() ЕуЕФзјБъ;ВЂЬНОП:дк
ЕуЕФзјБъ;ВЂЬНОП:дк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ,ЪЙ
,ЪЙ![]() ?ШєДцдкЃЌЧѓЕу
?ШєДцдкЃЌЧѓЕу![]() ЕФзјБъ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com