
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连接CE,AE,CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=10,BC=8,则线段CD的长为 .

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用圆周角定理结合等腰三角形的性质得出∠OCF+∠DCB=90°,即可得出答案;
(2)利用圆周角定理得出∠ACB=90°,利用相似三角形的判定与性质得出DC的长.
(1)证明:连接OC,
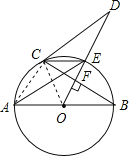
∵∠CEA=∠CBA,∠AEC=∠ODC,
∴∠CBA=∠ODC,
又∵∠CFD=∠BFO=90![]() ,
,
∴∠DCB=∠BOF,
∵CO=BO,
∴∠OCF=∠B,
∵∠B+∠BOF=90°,
∴∠OCF+∠DCB=90°,
∴直线CD为⊙O的切线;
(2)解:连接AC,

∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DCO=∠ACB=90°,
又∵∠D=∠B
∴△OCD∽△ACB,
∵∠ACB=90°,AB=10,BC=8,
∴AC=![]() 6,
6,
∴![]() ,即
,即![]() ,
,
解得;DC=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
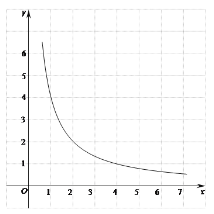
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.
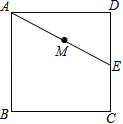
查看答案和解析>>
科目:初中数学 来源: 题型:
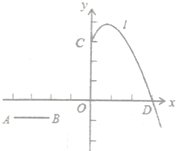
【题目】已知:如图,点![]() ,
,![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]()
(1)当![]() 时,求该抛物线与
时,求该抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)当![]() 时,求
时,求![]() 的最大值(用含
的最大值(用含![]() 的代数式表示);
的代数式表示);
(3)当抛物线![]() 经过点
经过点![]() 时,
时,![]() 的解析式为__________,顶点坐标为__________,点
的解析式为__________,顶点坐标为__________,点![]() __________(填“是”或“否”)在
__________(填“是”或“否”)在![]() 上.
上.
若线段![]() 以每秒2个单位长的速度向下平移,设平移的时间为
以每秒2个单位长的速度向下平移,设平移的时间为![]() (秒).
(秒).
①若![]() 与线段
与线段![]() 总有公共点,求
总有公共点,求![]() 的取值范围;
的取值范围;
②若![]() 同时以每秒3个单位长的速度向下平移,
同时以每秒3个单位长的速度向下平移,![]() 在
在![]() 轴及其右侧的图象与直线
轴及其右侧的图象与直线![]() 总有两个公共点,直接写出
总有两个公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数.图象
为常数.图象![]() ,
,![]() 合起来得到的图象记为
合起来得到的图象记为![]() .
.
(1)当![]() 时,
时,
①点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
②求图象![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)当图象![]() 的最低点到
的最低点到![]() 轴距离为
轴距离为![]() 时,求
时,求![]() 的值;
的值;
(3)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,
,![]() ,当图象
,当图象![]() 与线段
与线段![]() 有两个交点时,直接写出
有两个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.

(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
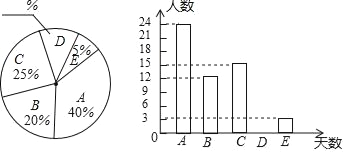
请根据以上的信息,回答下列问题:
(1)补全扇形统计图和条形统计图;
(2)所抽查学生参加社会实践活动天数的众数是 (选填:A、B、C、D、E);
(3)若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com