
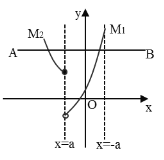
【题目】在平面直角坐标系中,函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数.图象
为常数.图象![]() ,
,![]() 合起来得到的图象记为
合起来得到的图象记为![]() .
.
(1)当![]() 时,
时,
①点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
②求图象![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)当图象![]() 的最低点到
的最低点到![]() 轴距离为
轴距离为![]() 时,求
时,求![]() 的值;
的值;
(3)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,
,![]() ,当图象
,当图象![]() 与线段
与线段![]() 有两个交点时,直接写出
有两个交点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②交点坐标
;②交点坐标![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①将a=2代入函数,求出函数解析式,再将点P代入即可解答;
②分两种情况分析,当x>2时和当![]() 时,分别解方程即可;
时,分别解方程即可;
(2)分两种情况,![]() 时以及
时以及![]() 时,分别画出图象,确定M2何时取最低点,再列出方程解答即可;
时,分别画出图象,确定M2何时取最低点,再列出方程解答即可;
(3)当![]() ,可分两种情况,分别画出图形,结合图形列出不等式;
,可分两种情况,分别画出图形,结合图形列出不等式;![]() ,画出图形,根据题意,结合图形,列出不等式即可解答.
,画出图形,根据题意,结合图形,列出不等式即可解答.
(1)①![]() 时,函数
时,函数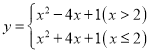 .
.
![]() 在图象上,代入
在图象上,代入![]() 中,得
中,得![]() ;
;
②当x>2时,![]() ,
,![]() ,
,![]() (舍)
(舍)
当![]() 时,
时,![]() 时,
时,![]() ,
,![]()
综上,交点坐标为![]() ,
,![]() ,
,![]() .
.
(2)![]() 时,图象如下所示,
时,图象如下所示,
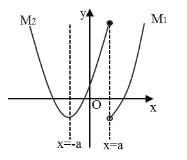
当![]() 时,
时,![]() 取最低点
取最低点
即![]() (方程无解),或
(方程无解),或![]()
解得![]() ,
,![]() (舍去).
(舍去).
![]() 时,图象如下所示,
时,图象如下所示,
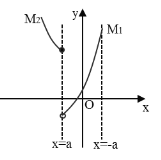
即![]() 时,
时,![]() 取最低点
取最低点
即![]() 或
或![]() (方程无解)
(方程无解)
![]() ,
,![]() (舍)
(舍)
综上,![]() 或
或![]() .
.
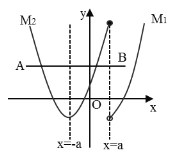
(3)①![]() ,如图所示,
,如图所示,
即![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
即![]() .
.
②![]() ,如下图所示,
,如下图所示,
即![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
即![]() .
.

③![]() ,如下图所示,
,如下图所示,
即![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() .
.
即![]() .
.
综上所述,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为非负整数,且该方程的根都是无理数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(![]() )求m的取值范围;
)求m的取值范围;
(![]() )若m取满足条件的最小的整数,
)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
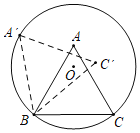
【题目】如图,正![]() 的边长为2,顶点
的边长为2,顶点![]() 、
、![]() 在半径为
在半径为![]() 的圆上,顶点
的圆上,顶点![]() 在圆内,将正
在圆内,将正![]() 绕点
绕点![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上时,则点
第一次落在圆上时,则点![]() 运动的路线长为__________(结果保留
运动的路线长为__________(结果保留![]() );若
);若![]() 点落在圆上记做第1次旋转,将
点落在圆上记做第1次旋转,将![]() 绕点
绕点![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上记做第2次旋转,再绕
第一次落在圆上记做第2次旋转,再绕![]() 将
将![]() 逆时针旋转,当点
逆时针旋转,当点![]() 第一次落在圆上,记做第3次旋转……,若此旋转下去,当
第一次落在圆上,记做第3次旋转……,若此旋转下去,当![]() 完成第2018次旋转时,
完成第2018次旋转时,![]() 边共回到原来位置__________次.
边共回到原来位置__________次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍,并且甲工程队完成300平方米的绿化面积比乙工程队完成300平方米的绿化面积少用3小时,乙工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连接CE,AE,CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=10,BC=8,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
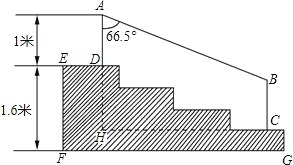
【题目】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°.
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米)
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 | 频数 | 频率 |
| 2 | 0.04 |
|
| 0.16 |
| 20 | 0.40 |
| 16 | 0.32 |
| 4 |
|
合计 | 50 | 1 |
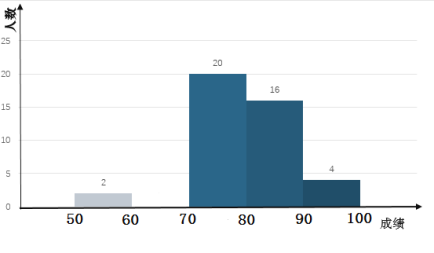
请你根据图表提供的信息,解答下列问题:
(1)求出![]() ,
,![]() 的值并补全频数分布直方图.
的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:![]() ;
;![]() ;
;![]() 若按照这样的分组方式绘制扇形统计图,则其中
若按照这样的分组方式绘制扇形统计图,则其中![]() 组所在扇形的圆心角的度数是多少?
组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 内接于⊙O,∠B=60°,CD 是⊙O 的直径,点 P 是 CD 延长线上的一点且 AP=AC.

(1)求证:PA 是⊙O 的切线;
(2)若![]() ,
,![]() ,求⊙O的半径
,求⊙O的半径
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com