
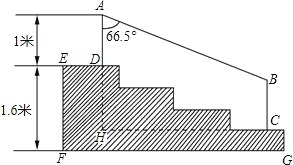
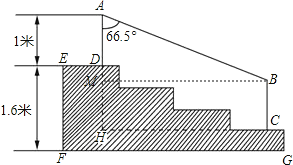
【题目】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°.
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米)
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
【答案】(1)DH=1.2米;(2)点D与点C的高度差DH为1.2米;所用不锈钢材料的总长度约为5.0米.
【解析】
(1)通过图观察可知DH高度包含3层台阶,因而DH=每级小台阶高度×小台阶层数.
(2)首先过点B作BM⊥AH,垂足为M.求得AM的长,在Rt△AMB中,根据余弦函数![]() 即可求得AB的长,那么根据不锈钢材料的总长度l=AD+AB+BC,求得所用不锈钢材料的长.
即可求得AB的长,那么根据不锈钢材料的总长度l=AD+AB+BC,求得所用不锈钢材料的长.
(1)DH=1.6×![]() =1.2(米);
=1.2(米);
(2)过B作BM⊥AH于M,则四边形BCHM是矩形.
∴MH=BC=1
∴AM=AH﹣MH=1+1.2﹣1=1.2.
在Rt△AMB中,∠A=66.5°.
∴AB=![]() (米).
(米).
∴l=AD+AB+BC≈1+3.0+1=5.0(米).
答:点D与点C的高度差DH为1.2米;所用不锈钢材料的总长度约为5.0米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
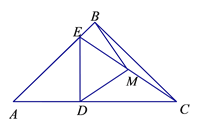

图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商贩用600元购进了一批水果,上市后销售非常好,商贩又用1400元购进第二批这种水果,所购水果数量是第一批购进数量的2倍,但每箱进价多了5元.
(1)求该商贩第一批购进水果每箱多少元;
(2)由于储存不当,第二批购进的水果中有10%腐坏,不能售卖,该商贩将两批水果按同一价格全部销售完毕后获利不低于800元,求每箱水果的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数.图象
为常数.图象![]() ,
,![]() 合起来得到的图象记为
合起来得到的图象记为![]() .
.
(1)当![]() 时,
时,
①点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
②求图象![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)当图象![]() 的最低点到
的最低点到![]() 轴距离为
轴距离为![]() 时,求
时,求![]() 的值;
的值;
(3)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,
,![]() ,当图象
,当图象![]() 与线段
与线段![]() 有两个交点时,直接写出
有两个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
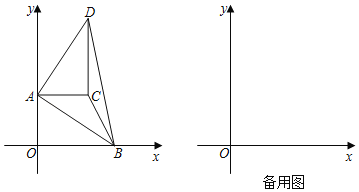
【题目】如图,在平面直角坐标系中,O为原点,点A(0,10),点B(m,0),且m>0,把△AOB绕点A逆时针旋转90°,得到△ACD,点O,B旋转后的对应点分别为点C,D.
(1)点C的坐标为 ;
(2)①设△BCD的面积为S,用含m的代数式表示S,并直接写出m的取值范围;
②当S=12时,请直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
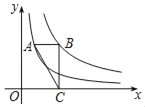
【题目】如图,点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
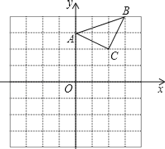
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是_______;
(2)△A1B1C1的面积是_______平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
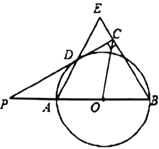
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com