
【题目】如图,在等腰![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连结
,连结![]() .
.
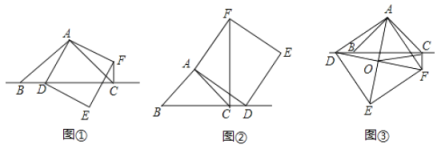
(猜想)如图①,当点![]() 在线段
在线段![]() 上时,直接写出
上时,直接写出![]() 、
、![]() 、
、![]() 三条线段的数量关系.
三条线段的数量关系.
(探究)如图②,当点![]() 在线段
在线段![]() 的延长线上时,判断
的延长线上时,判断![]() 、
、![]() 、
、![]() 三条线段的数量关系,并说明理由.
三条线段的数量关系,并说明理由.
(应用)如图③,当点![]() 在线段
在线段![]() 的反向延长线上时,点
的反向延长线上时,点![]() 、
、![]() 分别在直线
分别在直线![]() 两侧,
两侧,![]() 、
、![]() 交点为点
交点为点![]() 连结
连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() .
.
科目:初中数学 来源: 题型:
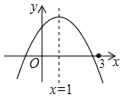
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,过
上一点,过![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
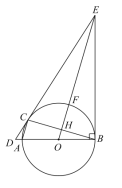
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
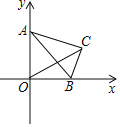
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,将含30°角的
为坐标原点,将含30°角的![]() 放在第一象限,其中30°角的对边
放在第一象限,其中30°角的对边![]() 长为1,斜边
长为1,斜边![]() 的端点
的端点![]() ,
,![]() 分别在
分别在![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴上滑动,连接
轴的正半轴上滑动,连接![]() ,则线段
,则线段![]() 的长的最大值是( )
的长的最大值是( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
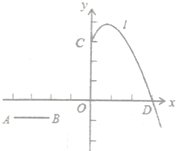
【题目】已知:如图,点![]() ,
,![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]()
(1)当![]() 时,求该抛物线与
时,求该抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)当![]() 时,求
时,求![]() 的最大值(用含
的最大值(用含![]() 的代数式表示);
的代数式表示);
(3)当抛物线![]() 经过点
经过点![]() 时,
时,![]() 的解析式为__________,顶点坐标为__________,点
的解析式为__________,顶点坐标为__________,点![]() __________(填“是”或“否”)在
__________(填“是”或“否”)在![]() 上.
上.
若线段![]() 以每秒2个单位长的速度向下平移,设平移的时间为
以每秒2个单位长的速度向下平移,设平移的时间为![]() (秒).
(秒).
①若![]() 与线段
与线段![]() 总有公共点,求
总有公共点,求![]() 的取值范围;
的取值范围;
②若![]() 同时以每秒3个单位长的速度向下平移,
同时以每秒3个单位长的速度向下平移,![]() 在
在![]() 轴及其右侧的图象与直线
轴及其右侧的图象与直线![]() 总有两个公共点,直接写出
总有两个公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.

(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
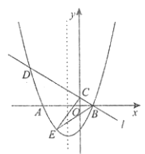
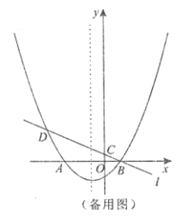
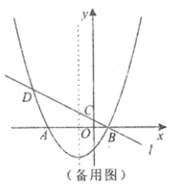
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() .
.
(1)则点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,抛物线的对称轴为__________;
的坐标为__________,抛物线的对称轴为__________;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,当
下方抛物线上的一点,当![]() 时.求
时.求![]() 面积的最大值;
面积的最大值;
(3)设![]() 为抛物线对称轴上一点,点
为抛物线对称轴上一点,点![]() 在抛物线上,若以点
在抛物线上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形,求
为顶点的四边形为矩形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com