
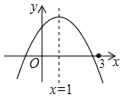
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
由抛物线的开口方向、对称轴位置、与y轴的交点位置判断出a、b、c与0的关系,进而判断①;根据抛物线对称轴为x=![]() =1判断②;根据函数的最大值为:a+b+c判断③;求出x=﹣1时,y<0,进而判断④;对ax12+bx1=ax22+bx2进行变形,求出a(x1+x2)+b=0,进而判断⑤.
=1判断②;根据函数的最大值为:a+b+c判断③;求出x=﹣1时,y<0,进而判断④;对ax12+bx1=ax22+bx2进行变形,求出a(x1+x2)+b=0,进而判断⑤.
解:①抛物线开口方向向下,则a<0,
抛物线对称轴位于y轴右侧,则a、b异号,即b>0,
抛物线与y轴交于正半轴,则c>0,
∴abc<0,故①错误;
②∵抛物线对称轴为直线x=![]() =1,
=1,
∴b=﹣2a,即2a+b=0,故②正确;
③∵抛物线对称轴为直线x=1,
∴函数的最大值为:a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,故③错误;
④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,故④错误;
⑤∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=﹣![]() ,
,
∵b=﹣2a,
∴x1+x2=2,故⑤正确.
综上所述,正确的是②⑤,有2个.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
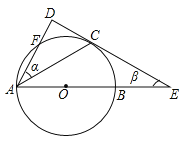
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
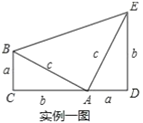
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由![]() 四边形
四边形![]() 得
得![]() ,化简得:
,化简得:![]() .
.
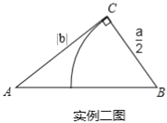
实例二:欧几里得的《几何原本》记载,关于![]() 的方程
的方程![]() 的图解法是:画
的图解法是:画![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜边
,再在斜边![]() 上截取
上截取![]() ,则
,则![]() 的长就是该方程的一个正根(如实例二图).
的长就是该方程的一个正根(如实例二图).
根据以上阅读材料回答下面的问题:
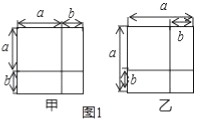
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是 ,体现的数学思想是 ;
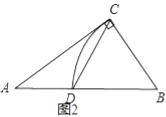
(2)如图2,按照实例二的方式构造![]() ,连接
,连接![]() ,请用含字母
,请用含字母![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长,
的长,![]() 的表达式能和已学的什么知识相联系;
的表达式能和已学的什么知识相联系;
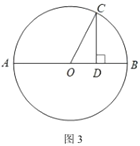
(3)如图3,已知![]() ,
,![]() 为直径,点
为直径,点![]() 为圆上一点,过点
为圆上一点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
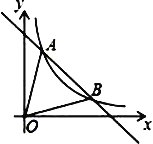
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y=kx-1(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中, G 为 BC 边上一点, BE AG 于 E , DF AG 于 F ,连接 DE .
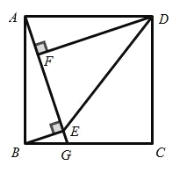
(1)求证: ABE DAF ;
(2)若 AF 1,四边形 ABED 的面积为6 ,求 EF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+2ax+c(a<0)的图象与x轴交于A、B两点,与y轴交于C点,顶点为D,一次函数y=mx﹣3的图象与y轴交于E点,与二次函数的对称轴交于F点,且tan∠FDC=![]() .
.
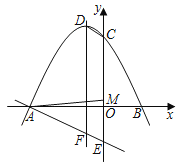
(1)求a的值;
(2)若四边形DCEF为平行四边形,求二次函数表达式.
(3)在(2)的条件下设点M是线段OC上一点,连接AM,点P从点A出发,先以1个单位长度/s的速度沿线段AM到达点M,再以![]() 个单位长度/s的速度沿MC到达点C,求点P到达点C所用最短时间为 s(直接写出答案).
个单位长度/s的速度沿MC到达点C,求点P到达点C所用最短时间为 s(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连结
,连结![]() .
.
(猜想)如图①,当点![]() 在线段
在线段![]() 上时,直接写出
上时,直接写出![]() 、
、![]() 、
、![]() 三条线段的数量关系.
三条线段的数量关系.
(探究)如图②,当点![]() 在线段
在线段![]() 的延长线上时,判断
的延长线上时,判断![]() 、
、![]() 、
、![]() 三条线段的数量关系,并说明理由.
三条线段的数量关系,并说明理由.
(应用)如图③,当点![]() 在线段
在线段![]() 的反向延长线上时,点
的反向延长线上时,点![]() 、
、![]() 分别在直线
分别在直线![]() 两侧,
两侧,![]() 、
、![]() 交点为点
交点为点![]() 连结
连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() .
.
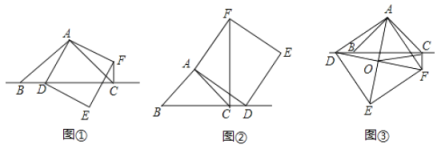
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com