
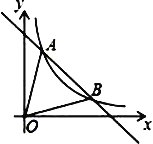
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y=kx-1(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积.
【答案】(1)![]() ;B(4,1);(2)S△AOB=
;B(4,1);(2)S△AOB=![]() .
.
【解析】
(1)由点A在一次函数图象上,可求出点A的坐标,结合点A的坐标,利用反比例函数图象上点的坐标特征即可求出反比例函数系数k的值,从而得出反比例函数解析式;联立一次函数解析式和反比例函数解析式,解方程组即可得出结论;
(2)设AB交x轴与点C,由一次函数解析式可求出点C的坐标,通过分割图形利用三角形的面积公式即可得出结论.
(1)∵一次函数y=x+5的图象过点A(1,n),
∴n=1+5,解得:n=4,
∴点A的坐标为(1,4),
∵反比例函数y=kx-1 (k≠0)过点A(1,4),
∴k=1×4=4,
∴反比例函数的解析式为:![]() .
.
联立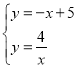 ,解得:
,解得:![]() 或
或![]() ,
,
∴点B的坐标为(4,1);
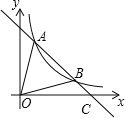
(2)设AB交x轴与点C,则C(5,0),如图所示,
∵A(1,4),B(4,1),
∴S△AOB=S△AOCS△BOC=![]() OCyA
OCyA![]() OCyB=
OCyB=![]() ×5×4
×5×4![]() ×5×1=
×5×1=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
统计数据,并制作了如下统计表:
时间 |
|
|
|
|
男生 | 2 |
|
| 4 |
女生 | 1 | 5 | 9 | 3 |
分析数据:两组数据的极差、平均数、中位数、众数如表所示
极差 | 平均数 | 中位数 | 方差 | ||
男生 | 77 | 66.7 |
| 70 | 617.3 |
女生 |
| 69.7 | 70.5 |
| 547.2 |
(1)请将上面的表格补充完整:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人?
(3)体育老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持体育老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若cosC=![]() ,AC=6,求BF的长.
,AC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
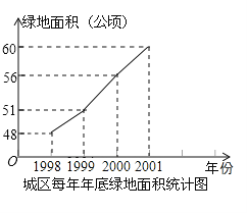
(1)根据图中所提供的信息,回答下列问题:2001年底的绿地面积为 公顷,比2000年底增加了 公顷;在1999年,2000年,2001年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2003年底使城区绿地总面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
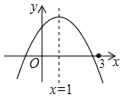
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
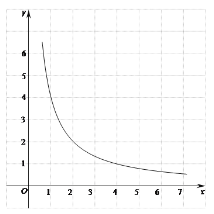
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连结CE,CF,若∠CEF=α,则tanα=_____.
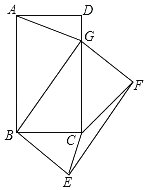
查看答案和解析>>
科目:初中数学 来源: 题型:
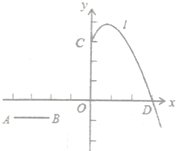
【题目】已知:如图,点![]() ,
,![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]()
(1)当![]() 时,求该抛物线与
时,求该抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)当![]() 时,求
时,求![]() 的最大值(用含
的最大值(用含![]() 的代数式表示);
的代数式表示);
(3)当抛物线![]() 经过点
经过点![]() 时,
时,![]() 的解析式为__________,顶点坐标为__________,点
的解析式为__________,顶点坐标为__________,点![]() __________(填“是”或“否”)在
__________(填“是”或“否”)在![]() 上.
上.
若线段![]() 以每秒2个单位长的速度向下平移,设平移的时间为
以每秒2个单位长的速度向下平移,设平移的时间为![]() (秒).
(秒).
①若![]() 与线段
与线段![]() 总有公共点,求
总有公共点,求![]() 的取值范围;
的取值范围;
②若![]() 同时以每秒3个单位长的速度向下平移,
同时以每秒3个单位长的速度向下平移,![]() 在
在![]() 轴及其右侧的图象与直线
轴及其右侧的图象与直线![]() 总有两个公共点,直接写出
总有两个公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com