
����Ŀ���������У��������ǵľ�ס�����ѳ�Ϊ���н����һ����Ҫ���ݣ�ij�г�������������ͨ����Ǩ�ɷ���ֲ�ݣ������������ȴ�ʩ��ʹ�����̵�����������ӣ���ͼ��ʾ��
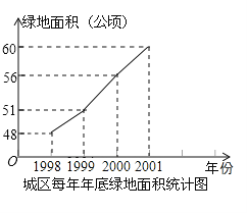
��1������ͼ�����ṩ����Ϣ���ش��������⣺2001����̵����Ϊ�� ���꣬��2000��������� ���ꣻ��1999�꣬2000�꣬2001���������У��̵�������������� �ꣻ
��2��Ϊ������з�չ����Ҫ���ƻ���2003���ʹ�����̵�������ﵽ72.6���꣬������������̵��������ƽ�������ʣ�
���𰸡���1��60��4��2000����2��10����
��������
��1����ϸ�۲�ͼ����ͼ������һһ���ɣ�
��2������ͼ���������֪�����г�һԪ���η��̣��ⷽ�̼��ɵó���.
�⣺��1������ͼ��֪��2001����̵����Ϊ60���꣬
2000���Ϊ56���꣬����2001��ױ�2000���������60-56=4�����꣩��
1998���Ϊ48���꣬1999���Ϊ51���꣬����1999��������51-48=3�����꣩
2000��������56-51=5�����꣩
5��4��3
��������������2000��.
��2������������̵��������ƽ��������Ϊx
�������⣬�� 60��1��x)2=72.6��
�����ã�1ʮx��2�� 1.21��
��������̣��� x1��0.l��x2=-2.l���������⣬��ȥ)
�𣺽��������̵��������ƽ��������Ϊ10����
�ʴ�Ϊ��1��60��4��2000����2��10����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+2ax+3a2+3������x���Ա���������x��2ʱ��y��x�������������-2��x��1ʱ��y�����ֵΪ9����a��ֵΪ![]() ����
����![]()
A. 1��![]() B. -
B. -![]() ��
��![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪������y��-x2��bx��c��x�ύ�ڵ�A(-1��0)��B(3��0)����y�ύ�ڵ�C��
(1)�������ߵĽ���ʽ��
(2)��D������Ϊ(1��0)����PΪ��һ�������������ϵ�һ�㣬���ı���BDCP��������ֵ��
(3)��ͼ�ڣ�����M�ӵ�O��������ÿ��2����λ���ȵ��ٶ����B�˶��������Bʱֹͣ�˶����Ҳ����O��B�غϣ����˶�ʱ��Ϊt�룬����M��x��Ĵ��߽��������ڵ�N�����߶�BC�ڵ�Q������OQ���Ƿ����tֵ��ʹ�á�BOQΪ���������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
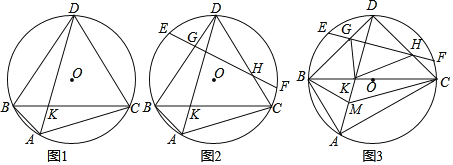
����Ŀ����֪��ABC�ڽ�����O��ADƽ�֡�BAC����O�ڵ�D����BC�ڵ�K������DB��DC��
��1����ͼ1����֤��DB��DC��
��2����ͼ2����E��F����O�ϣ�����EF��DB��DC�ڵ�G��H����DG��CH����֤��EG��FH��
��3����ͼ3���ڣ�2���������£�BC����Բ��O����AD��EF��BMƽ�֡�ABC��AD�ڵ�M��DK��![]() BM������GK��HK��CM������BDK���CKM�������Ϊ1�����ı���DGKH�������
BM������GK��HK��CM������BDK���CKM�������Ϊ1�����ı���DGKH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮
��x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮


��1�����A��B��C�����ꣻ
��2���趯��N����2��n������ʹMN��BN��ֵ��Сʱn��ֵ��
��3��P����������һ�㣬����̽�����Ƿ���ڵ�P��ʹ��P��A��BΪ��������������ABD���ƣ�����PAB���ABD���غϣ��������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
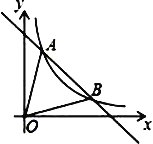
����Ŀ����ͼ��һ�κ���y=��x+5��ͼ���뷴��������y=kx-1��k��0���ڵ�һ����ͼ����A��1��n����B���㣮
��1�����������Ľ���ʽ���B���ꣻ
��2�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2��m��1��x+m2��3��0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����mΪ�Ǹ��������Ҹ÷��̵ĸ���������������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
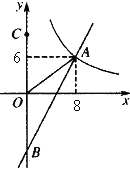
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��ֱ��뷴��������![]() ��ͼ���ڵ�һ�����ڵ�A��8��6������y��ĸ����ύ�ڵ�B����OA��OB.
��ͼ���ڵ�һ�����ڵ�A��8��6������y��ĸ����ύ�ڵ�B����OA��OB.
��1������y=kx+b��![]() �ı���ʽ��
�ı���ʽ��
��2����֪��C��0��10�������ڸ�һ�κ���ͼ����ȷ��һ��M��ʹ��MB��MC�����ʱ��M������.
�鿴�𰸺ͽ���>>
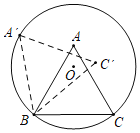
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ı߳�Ϊ2������
�ı߳�Ϊ2������![]() ��
��![]() �ڰ뾶Ϊ
�ڰ뾶Ϊ![]() ��Բ�ϣ�����
��Բ�ϣ�����![]() ��Բ�ڣ�����
��Բ�ڣ�����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת������
��ʱ����ת������![]() ��һ������Բ��ʱ�����
��һ������Բ��ʱ�����![]() �˶���·�߳�Ϊ__________���������
�˶���·�߳�Ϊ__________���������![]() ������
������![]() ������Բ�ϼ�����1����ת����
������Բ�ϼ�����1����ת����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת������
��ʱ����ת������![]() ��һ������Բ�ϼ�����2����ת������
��һ������Բ�ϼ�����2����ת������![]() ��
��![]() ��ʱ����ת������
��ʱ����ת������![]() ��һ������Բ�ϣ�������3����ת������������ת��ȥ����
��һ������Բ�ϣ�������3����ת������������ת��ȥ����![]() ��ɵ�2018����תʱ��
��ɵ�2018����תʱ��![]() �߹��ص�ԭ��λ��__________�Σ�
�߹��ص�ԭ��λ��__________�Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com