
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.


(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似,(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)令y=0可求得点A、点B的横坐标,令x=0可求得点C的纵坐标;
(2)根据两点之间线段最短作M点关于直线x=-2的对称点M′,当N(-2,N)在直线M′B上时,MN+BN的值最小;
(3)需要分类讨论:△PAB∽△ABD、△PAB∽△ABD,根据相似三角形的性质求得PB的长度,然后可求得点P的坐标.
(1)令y=0得x1=-2,x2=4,
∴点A(-2,0)、B(4,0)
令x=0得y=-![]() ,
,
∴点C(0,-![]() )
)
(2)将x=1代入抛物线的解析式得y=-![]()
∴点M的坐标为(1,-![]() )
)
∴点M关于直线x=-2的对称点M′的坐标为(-5,![]() )
)
设直线M′B的解析式为y=kx+b
将点M′、B的坐标代入得: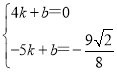
解得: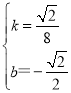 ,
,
所以直线M′B的解析式为y=![]() .
.
将x=-2代入得:y=-![]() ,
,
所以n=-![]() .
.
(3)过点D作DE⊥BA,垂足为E.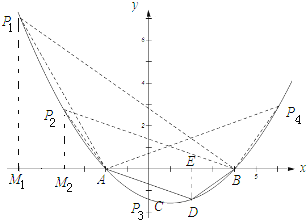
由勾股定理得:
AD=![]() ,
,
如下图,①当P1AB∽△ADB时,![]()
∴P1B=6![]()
过点P1作P1M1⊥AB,垂足为M1.
∴![]()
解得:P1M1=6![]() ,
,
∵![]()
解得:BM1=12
∴点P1的坐标为(-8,6![]() )或(12、6
)或(12、6![]() ).
).
∵点P1不在抛物线上,所以此种情况不存在;
②当△P2AB∽△BDA时,![]()
∴P2B=6![]() 过点P2作P2M2⊥AB,垂足为M2.
过点P2作P2M2⊥AB,垂足为M2.
∴![]()
∴P2M2=2![]()
∵![]()
∴M2B=8
∴点P2的坐标为(-4,2![]() )
)
将x=-4代入抛物线的解析式得:y=2![]() ,
,
∴点P2在抛物线上.
由抛物线的对称性可知:点P2与点P4关于直线x=1对称,
∴P4的坐标为(6,2![]() ),
),
当点P3位于点C处时,两三角形全等,所以点P3的坐标为(0,-![]() ),
),
综上所述点P的坐标为:(-4,2![]() )或(6,2
)或(6,2![]() )或(0,-
)或(0,-![]() )时,以P、A、B为顶点的三角形与△ABD相似.
)时,以P、A、B为顶点的三角形与△ABD相似.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
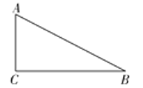
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用尺规作图法,作∠ACB的平分线CD,交AB于点D;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,过点D分别作 DE⊥AC于点E,DF⊥BC于点F.求证:四边形CEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
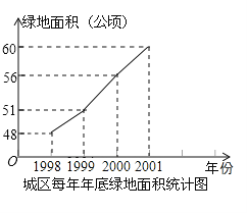
(1)根据图中所提供的信息,回答下列问题:2001年底的绿地面积为 公顷,比2000年底增加了 公顷;在1999年,2000年,2001年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2003年底使城区绿地总面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() ,
,![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() 时,若在函数值
时,若在函数值![]() 的情况下,只有一个自变量
的情况下,只有一个自变量![]() 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;
(3)当![]() 时,若在自变量
时,若在自变量![]() 的值满足
的值满足![]() ≤
≤![]() ≤
≤![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
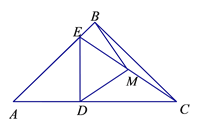
【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.

图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商贩用600元购进了一批水果,上市后销售非常好,商贩又用1400元购进第二批这种水果,所购水果数量是第一批购进数量的2倍,但每箱进价多了5元.
(1)求该商贩第一批购进水果每箱多少元;
(2)由于储存不当,第二批购进的水果中有10%腐坏,不能售卖,该商贩将两批水果按同一价格全部销售完毕后获利不低于800元,求每箱水果的售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com