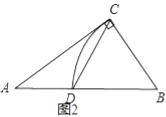
【题目】如图，
是
的直径，
是上一点，过作的切线，交
的延长线于点
，过
作
，交
延长线于点
，连接
，交于点
，交
于点
，连接
．
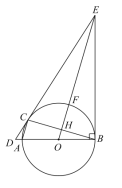
（1）求证：
；
（2）连接
，若
，
，求的长．
阳光试卷单元测试卷系列答案科目：初中数学 来源： 题型：
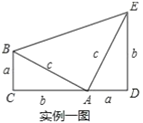
【题目】“构造图形解题”，它的应用十分广泛，特别是有些技巧性很强的题目，如果不能发现题目中所隐含的几何意义，而用通常的代数方法去思考，经常让我们手足无措，难以下手，这时，如果能转换思维，发现题目中隐含的几何条件，通过构造适合的几何图形，将会得到事半功倍的效果，下面介绍两则实例：
实例一：1876年，美国总统伽非尔德利用实例一图证明了勾股定理：由
四边形
得
，化简得：
．
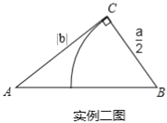
实例二：欧几里得的《几何原本》记载，关于
的方程
的图解法是：画
，使
，
，
，再在斜边
上截取，则
的长就是该方程的一个正根(如实例二图)．
根据以上阅读材料回答下面的问题：
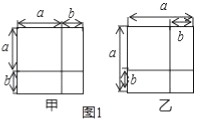
（1）如图1，请利用图形中面积的等量关系，写出甲图要证明的数学公式是 ，乙图要证明的数学公式是 ，体现的数学思想是 ；
（2）如图2，按照实例二的方式构造
，连接
，请用含字母
、
的代数式表示的长，的表达式能和已学的什么知识相联系；
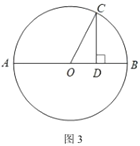
（3）如图3，已知
，为直径，点
为圆上一点，过点作
于点
，连接
，设
，
，求证：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A，B，C都在格点上．将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．
（1）在正方形网格中，画出△AB′C′；
（2）计算线段AB在变换到AB′的过程中扫过的区域的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y＝ax2+2ax+c（a＜0）的图象与x轴交于A、B两点，与y轴交于C点，顶点为D，一次函数y＝mx﹣3的图象与y轴交于E点，与二次函数的对称轴交于F点，且tan∠FDC＝
．
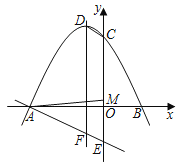
（1）求a的值；
（2）若四边形DCEF为平行四边形，求二次函数表达式．
（3）在（2）的条件下设点M是线段OC上一点，连接AM，点P从点A出发，先以1个单位长度/s的速度沿线段AM到达点M，再以
个单位长度/s的速度沿MC到达点C，求点P到达点C所用最短时间为 s（直接写出答案）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
的直径AB垂直弦CD于点E，过C点作CG∥AD交AB延长线于点G，连结CO并延长交AD于点F，且CF⊥AD．
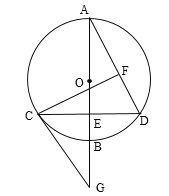
（1）求证：CG是⊙O的切线；
（2）若AB=4，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b交y轴于点A，交x轴于点B，S△AOB＝
．
（1）求b的值；
（2）点C以每秒1个单位长度的速度从O点出发沿x轴向点B运动，点D以每秒2个单位长度的速度从A点出发沿y轴向点O运动，C，D两点同时出发，当点D运动到点O时，C，D两点同时停止运动．连接CD，设点C的运动时间为t秒，△CDO的面积为S，求S与t的函数关系式（不要求写出自变量t的取值范围）；
（3）在（2）条件下，过点C作CE⊥CD交AB于点E，过点D作DF∥x轴交AB于点F，过点F作FH⊥CE，垂足为H．在CH上取点M，使得MH：HE＝8：33，连接FM，若∠FMH＝
∠FEH，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
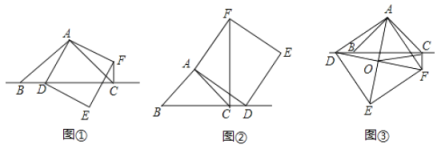
【题目】如图，在等腰
中，
点
为直线
上一动点(点不与
、
重合)．以
为边向右侧作正方形
，连结
．
（猜想）如图①，当点在线段上时，直接写出、、
三条线段的数量关系．
（探究）如图②，当点在线段的延长线上时，判断、、三条线段的数量关系，并说明理由．
（应用）如图③，当点在线段的反向延长线上时，点
、
分别在直线两侧，
、
交点为点
连结
，若
，
，则
．
查看答案和解析>>
科目：初中数学 来源： 题型：
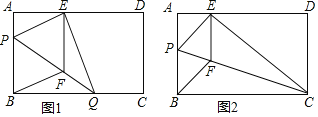
【题目】如图1，在矩形纸片ABCD中，AB＝12cm，AD＝20cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．
（1）求证：四边形BFEP为菱形；
（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
