
����Ŀ����ͼ1���ھ���ֽƬABCD�У�AB��12cm��AD��20cm���۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ������E��EF��AB��PQ��F������BF��
��1����֤���ı���BFEPΪ���Σ�
��2������E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���
�ٵ���Q���C�غ�ʱ����ͼ2����������BFEP�ı߳���
������P��Q�ֱ��ڱ�BA��BC���ƶ��������E�ڱ�AD���ƶ��������룮
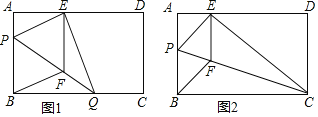
���𰸡���1��֤������������2��������BFEP�ı߳�Ϊ![]() cm���ڵ�E�ڱ�AD���ƶ���������Ϊ8cm��
cm���ڵ�E�ڱ�AD���ƶ���������Ϊ8cm��
��������
��1�����۵������ʵó�PB=PE��BF=EF����BPF=��EPF����ƽ���ߵ����ʵó���BPF=��EFP��֤����EPF=��EFP���ó�EP=EF�����BP=BF=EF=EP�����ɵó����ۣ�
��2�����ɾ��ε����ʵó�BC=AD=20cm��CD=AB=12cm����A=��D=90�����ɶԳƵ����ʵó�CE=BC=20cm����Rt��CDE�У��ɹ��ɶ������DE=16cm���ó�AE=AD-DE=4cm����Rt��APE�У��ɹ��ɶ����ó����̣��ⷽ�̵ó�EP=![]() cm���ɣ�
cm���ɣ�
�ڵ���Q���C�غ�ʱ����E���A������ɢ�֪����ʱAE=4cm������P���A�غ�ʱ����E���A��Զ����ʱ�ı���ABQEΪ�����Σ�AE=AB=3cm�����ɵó��𰸣�
��1��֤�������۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ��
���B���E����PQ�Գƣ�
��PB��PE��BF��EF����BPF����EPF��
�֡�EF��AB��
���BPF����EFP��
���EPF����EFP��
��EP��EF��
��BP��BF��EF��EP��
���ı���BFEPΪ���Σ�
��2���١��ı���ABCD�Ǿ��Σ�
��BC��AD��20cm��CD��AB��12cm����A����D��90����
�ߵ�B���E����PQ�Գƣ�
��CE��BC��20cm��
��Rt��CDE��DE��![]() ��16cm��
��16cm��
��AE��AD��DE��20cm��16cm��4cm��
��Rt��APE��AE��4��AP��12��PB��12��PE��
��EP2��42+��12��EP��2��
��ã�EP��![]() cm��
cm��
������BFEP�ı߳�Ϊ![]() cm��
cm��
�ڵ���Q���C�غ�ʱ����ͼ2��
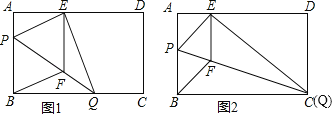
��E���A������ɢ�֪����ʱAE��4cm��
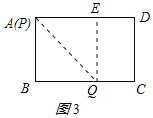
����P���A�غ�ʱ����ͼ3��ʾ��
��E���A��Զ����ʱ�ı���ABQEΪ�����Σ�AE��AB��12cm��
���E�ڱ�AD���ƶ���������Ϊ8cm



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() �����ߣ���
�����ߣ���![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
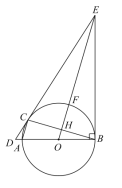
��1����֤��![]() ��
��
��2������![]() ����
����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�δ�����У�ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣���ͼ��ת�̱�ƽ���ֳ�![]() �ݣ������涨���˿�ÿ����
�ݣ������涨���˿�ÿ����![]() Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���
Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��![]() Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ
Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ![]() Ԫ��
Ԫ��

��1����ÿת��һ��ת��������ȯ����ƽ������
��2��������ڸ��̳�����![]() Ԫ�����ѡ��תת�̻���ֱ�ӻ�ù���ȯ��˵�����ɣ�
Ԫ�����ѡ��תת�̻���ֱ�ӻ�ù���ȯ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
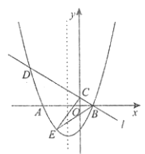
����Ŀ����ͼ����֪������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() (��
(��![]() �ڵ�
�ڵ�![]() �����)��������
�����)��������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵ���һ������Ϊ
���������ߵ���һ������Ϊ![]() ��
��
��1�����![]() ������Ϊ__________����
������Ϊ__________����![]() ������Ϊ__________�������ߵĶԳ���Ϊ__________��
������Ϊ__________�������ߵĶԳ���Ϊ__________��
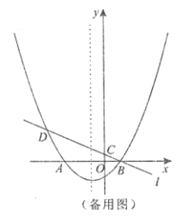
��2����![]() ��ֱ��
��ֱ��![]() �·��������ϵ�һ�㣬��
�·��������ϵ�һ�㣬��![]() ʱ����
ʱ����![]() ��������ֵ��
��������ֵ��
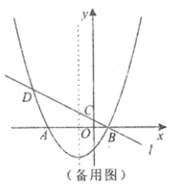
��3����![]() Ϊ�����߶Գ�����һ�㣬��
Ϊ�����߶Գ�����һ�㣬��![]() ���������ϣ����Ե�
���������ϣ����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊ���Σ���
Ϊ������ı���Ϊ���Σ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽Ȿ�����꼶ѧ�������ڼ�μ����ʵ���������������˲������꼶ѧ�����ٲμ����ʵ�������������A������������5��������B������6��������C������7��������D������8��������E������9�켰���������������õ������ݻ��Ƴ�����������������ͳ��ͼ��
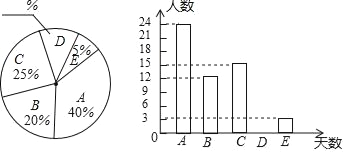
��������ϵ���Ϣ���ش��������⣺
��1����ȫ����ͳ��ͼ������ͳ��ͼ��
��2�������ѧ���μ����ʵ����������������� ����ѡ�A��B��C��D��E����
��3�����������꼶Լ��2000��ѧ����������Ʋμ����ʵ���������������7������ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ž�ͨ��·�IJ������ƣ�����������ҵ�ķ�չ��ij�����ξ�����A��B��C��D��E���������㣬�������β���ͳ�ƻ��Ƴ�2017�ꡰ��һ�������ڼ��������ͳ��ͼ������������Ϣ����������⣺

��1��2017�ꡰ��һ���ڼ䣬�����ܱ߾��㹲�Ӵ��ο� ���ˣ�����ͳ��ͼ��A��������Ӧ��Բ�ĽǵĶ����� ������ȫ����ͳ��ͼ��
��2�����ݽ����굽�������������������ƣ�Ԥ��2018�ꡰ��һ���ڽ���80���ο�ѡ��������Σ�������ж������˻�ѡ��ȥE�������Σ�
��3���ס���������������A��B��D���������У�ͬʱѡ��ȥͬһ����ĸ����Ƕ��٣����û���״ͼ���б�������˵�������о����õȿ��ܵĽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ����ѧ���ϴ���ͬѧ������ѧ��Ϸ���������£�
��Ϸ����
���α�һ���������������ң�
�Ұ��������![]() ������
������
���ٰ����õ����ľ���ֵ��������
���ٰ��������һ���![]() �������𰸣�
�������𰸣�
������Ϸ���ش���������⣺
��1�����ױ�����Ϊ![]() �����ұ�����Ϊ_________���������Ĵ���_________��
�����ұ�����Ϊ_________���������Ĵ���_________��
��2�����ױ�����Ϊ![]() �����г���ʽ�����㶡�����Ĵ𰸣�
�����г���ʽ�����㶡�����Ĵ𰸣�
��3�����������Ĵ���![]() ����ֱ��д���ױ�������
����ֱ��д���ױ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ��� ABCD �У�M��N��P��Q �ֱ�Ϊ�� AB��BC��CD��DA �ϵĵ㣨����˵��غϣ�������������� ABCD�������ĸ������У��ٴ����������ı��� MNPQ ��ƽ���ı��Σ��ڴ����������ı��� MNPQ �Ǿ��Σ��۴����������ı��� MNPQ �����Σ��ܲ������ı��� MNPQ �������Σ�������ȷ���۵������_________________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��8��BC��4����������AC�۵�����D���ڵ�D���������ص����֡�AFC�����Ϊ�� ��

A.6B.8C.10D.12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com