
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпyЃНЉx+bНЛyжсгкЕуAЃЌНЛxжсгкЕуBЃЌSЁїAOBЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓbЕФжЕЃЛ
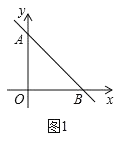
ЃЈ2ЃЉЕуCвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгOЕуГіЗЂбиxжсЯђЕуBдЫЖЏЃЌЕуDвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгAЕуГіЗЂбиyжсЯђЕуOдЫЖЏЃЌCЃЌDСНЕуЭЌЪБГіЗЂЃЌЕБЕуDдЫЖЏЕНЕуOЪБЃЌCЃЌDСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎСЌНгCDЃЌЩшЕуCЕФдЫЖЏЪБМфЮЊtУыЃЌЁїCDOЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
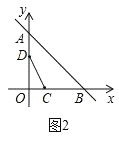
ЃЈ3ЃЉдкЃЈ2ЃЉЬѕМўЯТЃЌЙ§ЕуCзїCEЁЭCDНЛABгкЕуEЃЌЙ§ЕуDзїDFЁЮxжсНЛABгкЕуFЃЌЙ§ЕуFзїFHЁЭCEЃЌДЙзуЮЊHЃЎдкCHЩЯШЁЕуMЃЌЪЙЕУMHЃКHEЃН8ЃК33ЃЌСЌНгFMЃЌШєЁЯFMHЃН![]() ЁЯFEHЃЌЧѓtЕФжЕЃЎ
ЁЯFEHЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉbЃН9ЃЛЃЈ2ЃЉSЃНЉt2+![]() ЃЛЃЈ3ЃЉtЃН1
ЃЛЃЈ3ЃЉtЃН1
ЁОНтЮіЁП
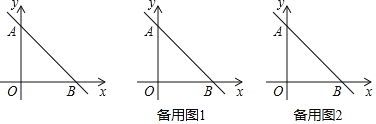
ЃЈ1ЃЉгЩжБЯпНтЮіЪНПЩЕУAЁЂBСНЕузјБъЃЌИљОнЁїAOBЕФУцЛ§СаЗНГЬНтГіbЕФжЕЃЎ
ЃЈ2ЃЉЗжБ№гУtБэЪОOCКЭODЕФГЄМДПЩЕУЕНSгыtЕФБэДяЪНЃЎ
ЃЈ3ЃЉЪзЯШИљОнЬтвтЛГіЪОвтЭМЃЌШЛКѓИљОнЫљИјЖЈЕФЯпЖЮЕШСПЙиЯЕгыНЧЖШЕШСПЙиЯЕЭЦЕМГіЁЯFEMЕФе§ЧажЕЃЌЙ§ЕуEзїGPЁЭOBгкPНЛDFЕФбгГЄЯпгкЕуGЃЌПЩвдЭЦжЄЁЯDEGЃНЁЯFEMЃЌгкЪЧРћгУЁЯDEGЕФе§ЧажЕСаГіБШР§ЗНГЬЃЌзюКѓНтГіtЕФжЕЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ
ЁпжБЯпyЃНЉx+bНЛyжсгкЕуAЃЌНЛxжсгкЕуBЃЌ
ЁрAЃЈ0ЃЌbЃЉЃЌBЃЈbЃЌ0ЃЉ
ЁрOAЃНOBЃНbЃЌ
ЁрSЁїAOBЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрbЃН9Лђ-9ЃЈВЛЗћКЯгыyжсЕФНЛЕуЃЌЩсШЅИКжЕЃЉЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌ
гЩЬтвтжЊOCЃНtЃЌADЃН2tЃЌдђODЃНOAЉADЃН9Љ2tЃЌ
ЁрSЃН![]() ODOCЃН
ODOCЃН![]() tЃЈ9Љ2tЃЉЃНЉt2+
tЃЈ9Љ2tЃЉЃНЉt2+![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЁп![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЩшMHЃН8kЃЌHEЃН33kЃЌ
ШчЭМ3ЃЌдкHEЩЯНиШЁHNЃНMHЃН8kЃЌСЌНгFNЃЌ
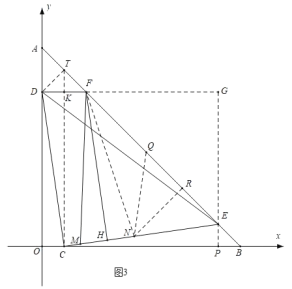
дђENЃНEHЉHNЃН25kЃЌ
ЁпFHЁЭCEгкHЃЌ
ЁрFMЃНFNЃЌЁЯFMEЃНЁЯFNMЃЌ
ЁпЁЯFMEЃН![]() ЁЯFEMЃЌ
ЁЯFEMЃЌ
ЁрЩшЁЯFEMЃН2ІСЃЌЁЯFMEЃН3ІСЃЌ
ЁрЁЯFNMЃН3ІСЃЌ
ЁпЁЯFNMЃНЁЯNFE+ЁЯFENЃЌ
ЁрЁЯNFEЃНЁЯFNMЉЁЯFEMЃН3ІСЉ2ІСЃНІСЃЌ
дкFEЩЯШЁвЛЕуQЃЌСЌНгNQЃЌЪЙNQЃНNEЃН25kЃЌ
дђЁЯNQEЃНЁЯFEMЃН2ІСЃЌ
ЁпЁЯNQEЃНЁЯNFE+ЁЯQNFЃНІС+ЁЯQNFЃЌ
ЁрЁЯNFЃНІСЃНЁЯNFEЃЌ
ЁрFQЃНNQЃН25kЃЌ
зїNRЁЭQEгкRЃЌдђQRЃНREЃНnЃЌ
ЁрFEЃНFQ+QEЃН25k+2nЃЌ
ЁпcosЁЯFEHЃНcos2ІСЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУnЃН15kЃЌ
ЁрQRЃНREЃН15kЃЌ
ЁрNRЃН![]() ЃН20kЃЌ
ЃН20kЃЌ
Ёрtan2ІСЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
Й§ЕуEзїGPЁЭOBгкPНЛDFЕФбгГЄЯпгкЕуGЃЌ
ЁрЁЯCPEЃНЁЯBPEЃН90ЁуЃЌ
ЁпOAЃНOBЃН9ЃЌ
ЁрЁЯOABЃНЁЯOBAЃН45ЁуЃЌ
ЁрЁЯPEBЃН45ЁуЃЌ
ЁрBPЃНPEЃЌ
ЁпDFЁЮOBЃЌ
ЁрЁЯODFЃНЁЯADFЃН90ЁуЃЌ
ЁрЫФБпаЮDOPGЮЊОиаЮЃЌ
ЁрGPЃНODЃЌDGЃНOPЃЌ
зїCTЁЭOBНЛABгкTЃЌНЛDFгкKЃЌСЌНгDTЃЌ
дђODKCЮЊОиаЮЃЌЁїCTBЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDKЃНOCЃНtЃЌCKЃНODЃЌCTЃНCBЃЌ
ЁпЁЯFDAЃН90ЁуЃЌЁЯFAFЃН45ЁуЃЌ
ЁрЁїADFЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDFЃНADЃН2OCЃН2tЃЌ
ЁрKЮЊDFжаЕуЃЌ
ЁрTЮЊAFжаЕуЃЌ
ЁрЁїDTFЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯDTKЃНЁЯFTKЃН45ЁуЃЌ
ЁпDCЁЭCEЃЌ
ЁрЁЯDCT+ЁЯTCEЃНЁЯTCE+ЁЯBCEЃН90ЁуЃЌ
ЁрЁЯDCTЃНЁЯECBЃЌ
дкЁїDCTКЭЁїECBжаЃК
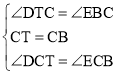
ЁрЁїDCTЁеЁїECBЃЈASAЃЉЃЌ
ЁрCDЃНCEЃЌ
ЁрЁїDCEЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯCEDЃН45ЁуЃЌ
ЁпЁЯDCO+ЁЯECPЃНЁЯDCO+ЁЯODCЃН90ЁуЃЌ
ЁрЁЯODCЃНЁЯECPЃЌ
дкЁїDOCКЭЁїCPEжаЃК
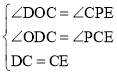
ЁрЁїDOCЁеЁїCPEЃЈAASЃЉЃЌ
ЁрBPЃНPEЃНOCЃНtЃЌ
ЁрDGЃНOPЃНOBЉPBЃН9ЉtЃЌ
ЁрFGЃНDGЉDFЃН9Љ3tЃЌ
ЁпЁЯGFEЃНЁЯAFDЃН45ЁуЃЌЁЯGEFЃНЁЯBEPЃН45ЁуЃЌ
ЁрDEЃНGFЃН9Љ3tЃЌ
ЁпЁЯDEGЃНЁЯFEG+ЁЯFEDЃН45Ёу+ЁЯFEDЃНЁЯDEC+ЁЯFEDЃНЁЯFEMЃН2ІСЃЌ
ЁрtanЁЯDEGЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУtЃН1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
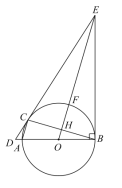
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBCНЛЁбOгкЕуDЃЌEЪЧ![]() ЕФжаЕуЃЌСЌНгAEНЛBCгкЕуFЃЌЁЯACB=2ЁЯEABЃЎ
ЕФжаЕуЃЌСЌНгAEНЛBCгкЕуFЃЌЁЯACB=2ЁЯEABЃЎ

ЃЈ1ЃЉЧѓжЄЃКACЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєcosC=![]() ЃЌAC=6ЃЌЧѓBFЕФГЄЃЎ
ЃЌAC=6ЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН5ЃЌBCЃН3ЃЌНЋОиаЮABCDШЦЕуBАДЫГЪБеыЗНЯђа§зЊЕУЕНОиаЮGBEFЃЌЕуAТфдкОиаЮABCDЕФБпCDЩЯЃЌСЌНсCEЃЌCFЃЌШєЁЯCEFЃНІСЃЌдђtanІСЃН_____ЃЎ
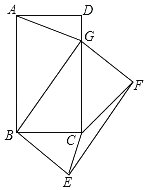
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌЙ§
ЩЯвЛЕуЃЌЙ§![]() зї
зї![]() ЕФЧаЯпЃЌНЛ
ЕФЧаЯпЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() ЃЌНЛ
ЃЌНЛ![]() бгГЄЯпгкЕу
бгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
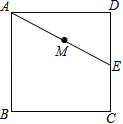
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ3cmЃЌEЮЊCDБпЩЯвЛЕуЃЌЁЯDAE=30ЁуЃЌMЮЊAEЕФжаЕуЃЌЙ§ЕуMзїжБЯпЗжБ№гыADЁЂBCЯрНЛгкЕуPЁЂQЃЎШєPQ=AEЃЌдђAPЕШгк cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌНЋКЌ30ЁуНЧЕФ
ЮЊзјБъдЕуЃЌНЋКЌ30ЁуНЧЕФ![]() ЗХдкЕквЛЯѓЯоЃЌЦфжа30ЁуНЧЕФЖдБп
ЗХдкЕквЛЯѓЯоЃЌЦфжа30ЁуНЧЕФЖдБп![]() ГЄЮЊ1ЃЌаББп
ГЄЮЊ1ЃЌаББп![]() ЕФЖЫЕу
ЕФЖЫЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дк
ЗжБ№дк![]() жсЕФе§АыжсЃЌ
жсЕФе§АыжсЃЌ![]() жсЕФе§АыжсЩЯЛЌЖЏЃЌСЌНг
жсЕФе§АыжсЩЯЛЌЖЏЃЌСЌНг![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ЕФГЄЕФзюДѓжЕЪЧЃЈ ЃЉ
ЕФГЄЕФзюДѓжЕЪЧЃЈ ЃЉ
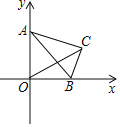
A.2B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() гы
гы![]() жсЦНааЃЌЧв
жсЦНааЃЌЧв![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓИУХзЮяЯпгы
ЪБЃЌЧѓИУХзЮяЯпгы![]() жсЕФНЛЕузјБъЃЛ
жсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФзюДѓжЕЃЈгУКЌ
ЕФзюДѓжЕЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉЕБХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЌ
ЪБЃЌ![]() ЕФНтЮіЪНЮЊ__________ЃЌЖЅЕузјБъЮЊ__________ЃЌЕу
ЕФНтЮіЪНЮЊ__________ЃЌЖЅЕузјБъЮЊ__________ЃЌЕу![]() __________ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉдк
__________ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉдк![]() ЩЯЃЎ
ЩЯЃЎ
ШєЯпЖЮ![]() вдУПУы2ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌЩшЦНвЦЕФЪБМфЮЊ
вдУПУы2ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌЩшЦНвЦЕФЪБМфЮЊ![]() ЃЈУыЃЉЃЎ
ЃЈУыЃЉЃЎ
ЂйШє![]() гыЯпЖЮ
гыЯпЖЮ![]() змгаЙЋЙВЕуЃЌЧѓ
змгаЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
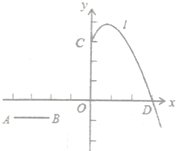
ЂкШє![]() ЭЌЪБвдУПУы3ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌ
ЭЌЪБвдУПУы3ИіЕЅЮЛГЄЕФЫйЖШЯђЯТЦНвЦЃЌ![]() дк
дк![]() жсМАЦфгвВрЕФЭМЯѓгыжБЯп
жсМАЦфгвВрЕФЭМЯѓгыжБЯп![]() змгаСНИіЙЋЙВЕуЃЌжБНгаДГі
змгаСНИіЙЋЙВЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛДЮДйЯњЛюЖЏжаЃЌФГЩЬГЁЮЊСЫЮќв§ЙЫПЭЃЌЩшСЂСЫвЛИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЈШчЭМЃЌзЊХЬБЛЦНОљЗжГЩ![]() ЗнЃЉЃЌВЂЙцЖЈЃКЙЫПЭУПЙКТђ
ЗнЃЉЃЌВЂЙцЖЈЃКЙЫПЭУПЙКТђ![]() дЊЕФЩЬЦЗЃЌОЭФмЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЎШчЙћзЊХЬЭЃжЙКѓЃЌжИеые§КУЖдзМКьЩЋЁЂЛЦЩЋЁЂТЬЩЋЧјгђЃЌФЧУДЙЫПЭОЭПЩвдЗжБ№ЛёЕУ
дЊЕФЩЬЦЗЃЌОЭФмЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЎШчЙћзЊХЬЭЃжЙКѓЃЌжИеые§КУЖдзМКьЩЋЁЂЛЦЩЋЁЂТЬЩЋЧјгђЃЌФЧУДЙЫПЭОЭПЩвдЗжБ№ЛёЕУ![]() дЊЁЂ
дЊЁЂ![]() дЊЁЂ
дЊЁЂ![]() дЊЕФЙКЮяШЏЃЌЦОЙКЮяШЏПЩвддкИУЩЬГЁМЬајЙКЮяЃЎШчЙћЙЫПЭВЛдИвтзЊзЊХЬЃЌФЧУДПЩвджБНгЛёЕУЙКЮяШЏ
дЊЕФЙКЮяШЏЃЌЦОЙКЮяШЏПЩвддкИУЩЬГЁМЬајЙКЮяЃЎШчЙћЙЫПЭВЛдИвтзЊзЊХЬЃЌФЧУДПЩвджБНгЛёЕУЙКЮяШЏ![]() дЊЃЎ
дЊЃЎ

ЃЈ1ЃЉЧѓУПзЊЖЏвЛДЮзЊХЬЫљЛёЙКЮяШЏН№ЖюЕФЦНОљЪ§ЃЛ
ЃЈ2ЃЉШчЙћФудкИУЩЬГЁЯћЗб![]() дЊЃЌФуЛсбЁдёзЊзЊХЬЛЙЪЧжБНгЛёЕУЙКЮяШЏЃПЫЕУїРэгЩЃЎ
дЊЃЌФуЛсбЁдёзЊзЊХЬЛЙЪЧжБНгЛёЕУЙКЮяШЏЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕРЯЪІдкЪ§бЇПЮЩЯДјСьЭЌбЇУЧзіЪ§бЇгЮЯЗЃЌЙцдђШчЯТЃК
гЮЯЗЙцдђ
МзШЮБЈвЛИігаРэЪ§Ъ§ДЋИјввЃЛ
ввАбетИіЪ§Мѕ![]() КѓБЈИјБћЃЛ
КѓБЈИјБћЃЛ
БћдйАбЫљЕУЕФЪ§ЕФОјЖджЕБЈИјЖЁЃЛ
ЖЁдйАбетИіЪ§ЕФвЛАыМѕ![]() ЃЌБЈГіД№АИЃЎ
ЃЌБЈГіД№АИЃЎ
ИљОнгЮЯЗЙцдђЃЌЛиД№ЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉШєМзБЈЕФЪ§ЮЊ![]() ЃЌдђввБЈЕФЪ§ЮЊ_________ЃЌЖЁБЈГіЕФД№АИЪЧ_________ЃЛ
ЃЌдђввБЈЕФЪ§ЮЊ_________ЃЌЖЁБЈГіЕФД№АИЪЧ_________ЃЛ
ЃЈ2ЃЉШєМзБЈЕФЪ§ЮЊ![]() ЃЌЧыСаГіЫуЪНВЂМЦЫуЖЁБЈГіЕФД№АИЃЛ
ЃЌЧыСаГіЫуЪНВЂМЦЫуЖЁБЈГіЕФД№АИЃЛ
ЃЈ3ЃЉШєЖЁБЈГіЕФД№АИЪЧ![]() ЃЌдђжБНгаДГіМзБЈЕФЪ§ЃЎ
ЃЌдђжБНгаДГіМзБЈЕФЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com