【题目】如图，六边形
的六个内角都等于
，若
，
，则这个六边形的周长等于____
.
【答案】17
【解析】
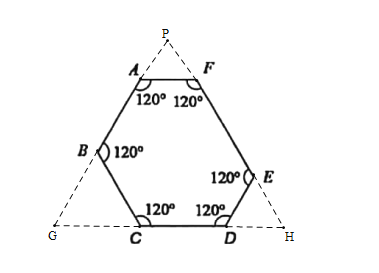
分别作直线AB、CD、EF的延长线使它们交于点G、H、P，根据题意推出三角形APF、三角形BGC、三角形DHE、三角形GHP都是等边三角形，接着求出大等边三角形的边长，从而求出AF,EF的长，即可求得周长.
如图，分别作直线AB、CD、EF的延长线使它们交于点G、H、P.
因为六边形ABCDEF的六个角都是
，
所以六边形ABCDEF的每一个外角的度数都是
.
所以三角形APF、三角形BGC、三角形DHE、三角形GHP都是等边三角形.
所以GC=BC=3cm，DH=DE=2cm.
所以GH=3+3+2=8cm，FA=PA=PGABBG=833=2cm，EF=PHPFEH=822=4cm.
所以六边形的周长为3+3+3+2+4+2=17cm.
科目：初中数学 来源： 题型：
【题目】如图四边形ABCD中，AD∥BC，∠BCD=90°，AB=BC+AD，∠DAC=45°，E为CD上一点，且∠BAE=45°．若CD=4，则△ABE的面积为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系中有三点A（﹣2，1）、B（3，1）、C（2，3）．请回答如下问题：
（1）在坐标系内描出点A、B、C的位置，并求△ABC的面积；
（2）在平面直角坐标系中画出△A′B′C′，使它与△ABC关于x轴对称，并写出△A′B′C′三顶点的坐标；
（3）若M（x，y）是△ABC内部任意一点，请直接写出这点在△A′B′C′内部的对应点M′的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8．
（1）求证：四边形ABCD是菱形；
（2）过点A作AH⊥BC于点H，求AH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示的正整数后，背面向上，洗匀放好．
（1）我们知道，满足a2+b2=c2的三个正整数a，b，c成为勾股数，嘉嘉从中随机抽取一张，求抽到的卡片上的数是勾股数的概率P1；
（2）琪琪从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张（卡片用A，B，C，D表示）．请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2，并指出她与嘉嘉抽到勾股数的可能性一样吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在锐角三角形ABC中，直线l为BC的中垂线，射线m为∠ABC的角平分线，直线l与m相交于点P.若∠BAC＝60°，∠ACP＝24°，则∠ABP的度数是( )
A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2016山东省济宁市）如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB=
，反比例函数
在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于（ ）
A. 60B. 80C. 30D. 40
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，A、B为x轴上两点，C、D为y轴上的两点，经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封
闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线C2：
（
＜0）的顶点．
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com