
【题目】如图,在正方形![]() 中,点
中,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正确的是( ).
.正确的是( ).

A.①②B.①③C.①③④D.③④
【答案】C
【解析】
连接![]() .根据“HL”可证
.根据“HL”可证![]() ≌
≌![]() ,利用全等三角形的对应边相等,可得
,利用全等三角形的对应边相等,可得![]() ,据此判断①;根据“
,据此判断①;根据“![]() ”可证
”可证![]() ≌
≌![]() ,可得
,可得![]() ,从而可得
,从而可得![]() ,据此判断②;由(2)知
,据此判断②;由(2)知![]() ,可证
,可证![]() ,据此判断③;根据两角分别相等的两个三角形相似,可证
,据此判断③;根据两角分别相等的两个三角形相似,可证![]() ∽
∽![]() ∽
∽![]() ,可得
,可得![]() , 从而可得
, 从而可得![]() ,据此判断④.
,据此判断④.
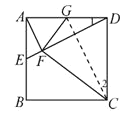
解:(1)连接![]() . 如图所示:
. 如图所示:
∵四边形ABCD是正方形,
∴∠ADC=90°,
∵FG⊥FC,
∴∠GFC=90°,
在Rt△CFG与Rt△CDG中,![]()
∴![]() ≌
≌![]() .
.
∴![]() ...①正确.
...①正确.
(2)由(1),![]() 垂直平分
垂直平分![]() .∴∠EDC+∠2=90°,
.∴∠EDC+∠2=90°,
∵∠1+∠EDC=90°,
∴![]() .
.
∵四边形ABCD是正方形,
∴AD=DC=AB,∠DAE=∠CDG=90°,
∴![]() ≌
≌![]() .
.
∴![]() .
.
∵![]() 为
为![]() 边的中点,
边的中点,
∴![]() 为
为![]() 边的中点.
边的中点.
∴![]() .∴②错误.
.∴②错误.
(3)由(2),得![]() . ∴
. ∴![]() .③正确.
.③正确.
(4)由(3),可得![]() ∽
∽![]() ∽
∽![]() . ∴
. ∴ ![]()
∴![]() . ∴④正确.
. ∴④正确.
故答案为:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
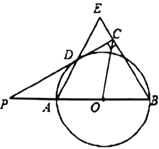
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
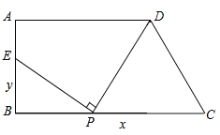
【题目】如图:梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=6,在线段BC上任取一点P,连接DP,作射线PE⊥DP,PE与直线AB交于点E.
(1)试确定当CP=3时,点E的位置;
(2)若设CP=x,BE=y,试写出y关于自变量x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里有材质、形状、大小完全相同的4个小球,它们的表面分别印有1、2、3、4四个数字(每个小球只印有一个数字),小华从布袋里随机摸出一个小球,把该小球上的数字记为![]() ,小刚从剩下的3个小球中随机摸出一个小球,把该小球上的数字记为
,小刚从剩下的3个小球中随机摸出一个小球,把该小球上的数字记为![]() .
.
(1)若小华摸出的小球上的数字是2,求小刚摸出的小球上的数字是3的概率;
(2)利用画树状图或列表格的方法,求点![]() 在函数
在函数![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产,已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为2.8万元,乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com