
【题目】以矩形![]() 的顶点
的顶点![]() 为坐标原点建立平面直角坐标系,使点
为坐标原点建立平面直角坐标系,使点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,双曲线
轴的正半轴上,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,过
,过![]() 边上一点
边上一点![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在矩形内部的一点
落在矩形内部的一点![]() 处,且
处,且![]() ,若点
,若点![]() 的坐标为(2,4),则
的坐标为(2,4),则![]() 的值为______.
的值为______.
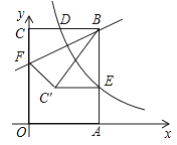
【答案】![]()
【解析】
延长E![]() 交OC于点G,设点D的坐标为(a,
交OC于点G,设点D的坐标为(a,![]() ),根据矩形的性质和反比例函数的特征即可证出点E为AB的中点,然后根据点
),根据矩形的性质和反比例函数的特征即可证出点E为AB的中点,然后根据点![]() 的坐标和折叠的性质即可各线段之间的关系,最后利用勾股定理列出方程即可求出CF和BC,最后根据正切的定义计算即可.
的坐标和折叠的性质即可各线段之间的关系,最后利用勾股定理列出方程即可求出CF和BC,最后根据正切的定义计算即可.
解:延长E![]() 交OC于点G
交OC于点G
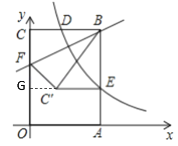
∵四边形OABC为矩形,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,设点D的坐标为(a,
,设点D的坐标为(a,![]() )
)
∴点B的坐标为(2a,![]() ),即BC=2a
),即BC=2a
∴点E的坐标为(2a,![]() ),EG=BC=2a
),EG=BC=2a
∴点E为AB的中点
∵![]() ,若点
,若点![]() 的坐标为(2,4),
的坐标为(2,4),
∴OG=AE=BE=4,OC=AB=2AE=8,![]()
由折叠性质可知:CF=![]() F,B
F,B![]() =BC=2a
=BC=2a
∴FG=OC-OG-CF=4-CF,![]() E=EG-
E=EG-![]() =2a-2
=2a-2
根据勾股定理可得:FG2+![]() 2=
2=![]() F2,
F2,![]() E 2+BE 2= B
E 2+BE 2= B![]() 2,
2,
即(4-CF)2+22= CF 2,(2a-2) 2+4 2= (2a)2,
解得:CF=![]() ,a=
,a=![]()
∴BC=2×![]() =5
=5
∴![]() =
=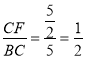
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】王老师在数学课上带领同学们做数学游戏,规则如下:
游戏规则
甲任报一个有理数数传给乙;
乙把这个数减![]() 后报给丙;
后报给丙;
丙再把所得的数的绝对值报给丁;
丁再把这个数的一半减![]() ,报出答案.
,报出答案.
根据游戏规则,回答下面的问题:
(1)若甲报的数为![]() ,则乙报的数为_________,丁报出的答案是_________;
,则乙报的数为_________,丁报出的答案是_________;
(2)若甲报的数为![]() ,请列出算式并计算丁报出的答案;
,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是![]() ,则直接写出甲报的数.
,则直接写出甲报的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里有材质、形状、大小完全相同的4个小球,它们的表面分别印有1、2、3、4四个数字(每个小球只印有一个数字),小华从布袋里随机摸出一个小球,把该小球上的数字记为![]() ,小刚从剩下的3个小球中随机摸出一个小球,把该小球上的数字记为
,小刚从剩下的3个小球中随机摸出一个小球,把该小球上的数字记为![]() .
.
(1)若小华摸出的小球上的数字是2,求小刚摸出的小球上的数字是3的概率;
(2)利用画树状图或列表格的方法,求点![]() 在函数
在函数![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
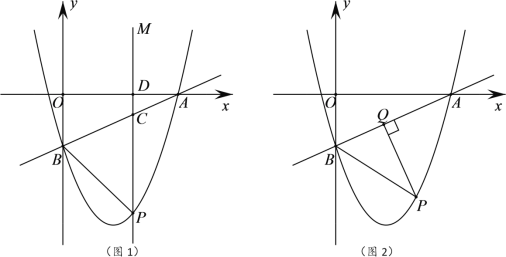
(1)求此抛物线对应的函数表达式;
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,规定点
轴的正方向运动,规定点![]() 到达点
到达点![]() 时,点
时,点![]() 停止运动,点
停止运动,点![]() 也停止运动.连接
也停止运动.连接![]() ,过点
,过点![]() 作
作![]() 的垂线,与过点
的垂线,与过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 相交于点D,
相交于点D,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() .
.
(1)求![]() 的度数及点
的度数及点![]() 的坐标(用
的坐标(用![]() 表示).
表示).
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)探索![]() 周长是否随时间
周长是否随时间![]() 的变化而变化.若变化,说明理由;若不变,试求出这个定值.
的变化而变化.若变化,说明理由;若不变,试求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com