
【题目】如图,正方形![]() 的边
的边![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,规定点
轴的正方向运动,规定点![]() 到达点
到达点![]() 时,点
时,点![]() 停止运动,点
停止运动,点![]() 也停止运动.连接
也停止运动.连接![]() ,过点
,过点![]() 作
作![]() 的垂线,与过点
的垂线,与过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 相交于点D,
相交于点D,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() .
.
(1)求![]() 的度数及点
的度数及点![]() 的坐标(用
的坐标(用![]() 表示).
表示).
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)探索![]() 周长是否随时间
周长是否随时间![]() 的变化而变化.若变化,说明理由;若不变,试求出这个定值.
的变化而变化.若变化,说明理由;若不变,试求出这个定值.
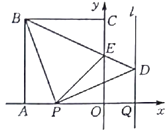
【答案】(1)![]() (2)当
(2)当![]() 为4秒或
为4秒或![]() 秒时,
秒时,![]() 为等腰三角形(3)周长是定值,该定值为8
为等腰三角形(3)周长是定值,该定值为8
【解析】
(1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标.
(2)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.由于△PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.
(3)由(2)已证的结论EP=AP+CE很容易得到△POE周长等于AO+CO=8,从而解决问题.
(1)
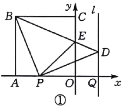
如图①.由题可得![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,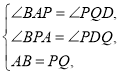
![]() .
.![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.![]() 点
点![]() 坐标为
坐标为![]() .
.
(2)①若![]() ,则
,则![]() .
.![]() .
.
![]() ,
,![]() .
.
![]() 点
点![]() 与点
与点![]() 重合.
重合.
![]() 点
点![]() 与点
与点![]() 重合.与条件“
重合.与条件“![]() 轴”矛盾,
轴”矛盾,
![]() 这种情况应舍去.
这种情况应舍去.
②若![]() ,则
,则![]() .
.![]() .
.
![]() .
.
在![]() 和
和![]() 中,
中,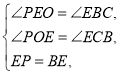
![]() ≌
≌![]() .
.![]() ,
,![]() .
.![]() .
.
![]() 点
点![]() 与点
与点![]() 重合(
重合(![]() ).
).![]() 点
点![]() 与点
与点![]() 重合(
重合(![]() ).
).
![]() 点
点![]() ,
,![]() .此时
.此时![]() .
.
③若![]() ,
,
在![]() 和
和![]() 中,
中,![]()
![]() .
.
![]() .
.![]() ,
,![]() .
.![]() .
.
![]() ,
,![]() .
.
延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,如图②所示.
,如图②所示.
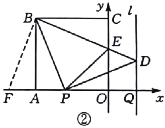
在![]() 和
和![]() 中,
中,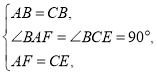
![]() .
.![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() .
.![]() .
.
在![]() 和
和![]() 中,
中,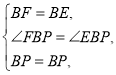
![]() .
.
![]() .
.![]() .
.
![]() .
.
![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 为4秒或
为4秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.
(3)![]() ,
,
![]() .
.
![]() 周长是定值,该定值为8.
周长是定值,该定值为8.


科目:初中数学 来源: 题型:
【题目】解不等式组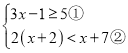
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
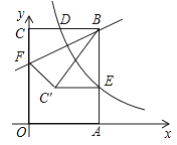
【题目】以矩形![]() 的顶点
的顶点![]() 为坐标原点建立平面直角坐标系,使点
为坐标原点建立平面直角坐标系,使点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,双曲线
轴的正半轴上,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,过
,过![]() 边上一点
边上一点![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在矩形内部的一点
落在矩形内部的一点![]() 处,且
处,且![]() ,若点
,若点![]() 的坐标为(2,4),则
的坐标为(2,4),则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() 在
在![]() 轴上,以点
轴上,以点![]() 为直角顶点作等腰直角
为直角顶点作等腰直角![]() ..当点
..当点![]() 落在某函数的图象上时,称点
落在某函数的图象上时,称点![]() 为该函数的“悬垂点”,
为该函数的“悬垂点”,![]() 为该函数的“悬垂等腰直角三角形”.
为该函数的“悬垂等腰直角三角形”.
(1)若点![]() 是函数
是函数![]() 的悬垂点,直接写出点
的悬垂点,直接写出点![]() 的横坐标为________.
的横坐标为________.
(2)若反比例函数![]()
![]() 的悬垂等腰直角三角形面积是
的悬垂等腰直角三角形面积是![]() ,求
,求![]() 的值.
的值.
(3)对于函数![]() ,当
,当![]()
![]() 时,该函数的悬垂点只有一个,求
时,该函数的悬垂点只有一个,求![]() 的取值范围.
的取值范围.
(4)若函数![]() 的悬垂等腰直角
的悬垂等腰直角![]() 的面积范围为
的面积范围为![]() ,且点
,且点![]() 在第一象限,直接写出
在第一象限,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
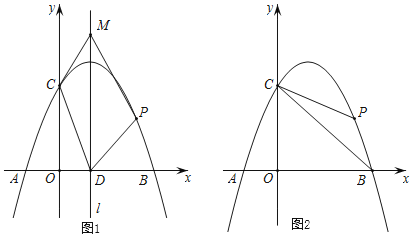
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
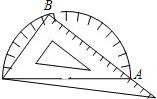
【题目】小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°和106°,由此可知三角板的较短直角边的长度为 cm.(参考数据:tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
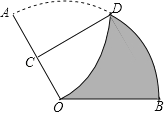
A.9![]() B.12π﹣9
B.12π﹣9![]() C.
C.![]() D.6π﹣
D.6π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的![]() .(保留作图痕迹)
.(保留作图痕迹)
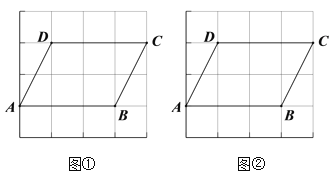
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com