
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)求此抛物线对应的函数表达式;
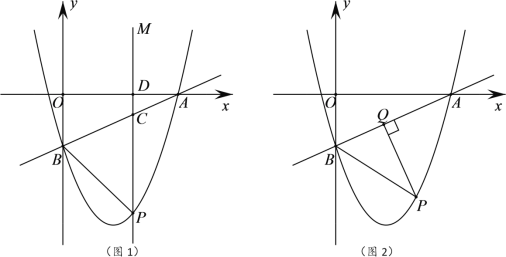
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
【答案】(1)抛物线对应的函数表达式为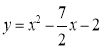 ;(2)P的坐标为
;(2)P的坐标为![]() 或
或![]() ;(3)点P的横坐标为3或
;(3)点P的横坐标为3或![]() .
.
【解析】
(1)先利用一次函数求出A,B两点的坐标,然后用待定系数法即可求出抛物线的表达式;
(2)分两种情况:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,分情况进行讨论即可;
,分情况进行讨论即可;
(3)分两种情况,![]() 和
和![]() ,分情况进行讨论即可.
,分情况进行讨论即可.
(1)令![]() 时,
时,![]() ,
,
∴![]() ,
,
令![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() ,
,
将点A,B代入![]() 中得
中得
![]() 解得
解得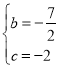
∴抛物线对应的函数表达式为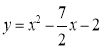 .
.
(2)设![]() ,
,
若![]() ,则
,则![]() ,
,
此时P点的纵坐标与B点的纵坐标相同,
∴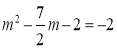 ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
∴![]() ,
,
若![]() ,则
,则![]() ,作PQ⊥OB于点Q,
,作PQ⊥OB于点Q,
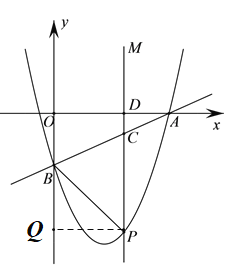
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
即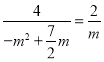 ,
,
解得![]() (舍去)或
(舍去)或![]()
∴![]()
综上所述,P的坐标为![]() 或
或![]() .
.
(3)若![]() ,过点B作BC∥OA交PQ于点C,过点P作PD⊥OB于点D
,过点B作BC∥OA交PQ于点C,过点P作PD⊥OB于点D
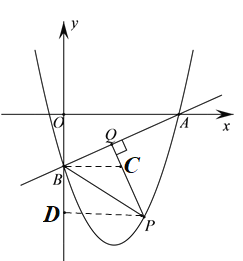
∵BC∥OA
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]()
∴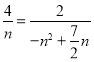
解得![]() (舍去)或
(舍去)或![]()
∴![]()
若![]() ,如图,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,过O作OF⊥AB于F,连接AP,则∠BPQ=∠OEF,
,如图,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,过O作OF⊥AB于F,连接AP,则∠BPQ=∠OEF,
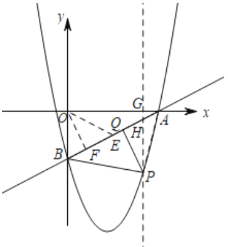
设点![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
则有![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即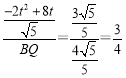 ,
,
![]()
![]() ,
,
![]() ,
,
化简得:![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
综上,存在点P,使得△PBQ中有某个角的度数等于∠OAB度数的2倍时,其P点的横坐标为3或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() ,且
,且![]() ,点
,点![]() 在射线
在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且满足
重合),且满足![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .设
.设![]()
![]() .
.
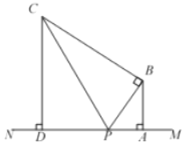
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)①线段![]() 的长是________;
的长是________;
②线段![]() 的长是_________;(用含
的长是_________;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 为何值时,
为何值时,![]() 有最小值?并求出这个最小值.
有最小值?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
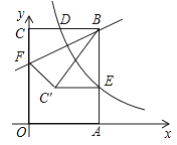
【题目】以矩形![]() 的顶点
的顶点![]() 为坐标原点建立平面直角坐标系,使点
为坐标原点建立平面直角坐标系,使点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,双曲线
轴的正半轴上,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,过
,过![]() 边上一点
边上一点![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在矩形内部的一点
落在矩形内部的一点![]() 处,且
处,且![]() ,若点
,若点![]() 的坐标为(2,4),则
的坐标为(2,4),则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
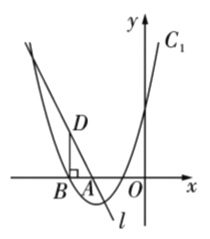
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 作
作![]() 垂直
垂直![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
(1)求抛物线的函数表达式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①求点![]() 的坐标;
的坐标;
②将拋物线![]() 向右平移使它经过点
向右平移使它经过点![]() ,此时得到的抛物线记为
,此时得到的抛物线记为![]() ,求出抛物线
,求出抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() 在
在![]() 轴上,以点
轴上,以点![]() 为直角顶点作等腰直角
为直角顶点作等腰直角![]() ..当点
..当点![]() 落在某函数的图象上时,称点
落在某函数的图象上时,称点![]() 为该函数的“悬垂点”,
为该函数的“悬垂点”,![]() 为该函数的“悬垂等腰直角三角形”.
为该函数的“悬垂等腰直角三角形”.
(1)若点![]() 是函数
是函数![]() 的悬垂点,直接写出点
的悬垂点,直接写出点![]() 的横坐标为________.
的横坐标为________.
(2)若反比例函数![]()
![]() 的悬垂等腰直角三角形面积是
的悬垂等腰直角三角形面积是![]() ,求
,求![]() 的值.
的值.
(3)对于函数![]() ,当
,当![]()
![]() 时,该函数的悬垂点只有一个,求
时,该函数的悬垂点只有一个,求![]() 的取值范围.
的取值范围.
(4)若函数![]() 的悬垂等腰直角
的悬垂等腰直角![]() 的面积范围为
的面积范围为![]() ,且点
,且点![]() 在第一象限,直接写出
在第一象限,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D四点都在OO上,弧AC=弧BC,连接AB,CD、AD,∠ADC=45°.
(1)如图1,AB是⊙O的直径;
(2)如图2,过点B作BE⊥CD于点E,点F在弧AC上,连接BF交CD于点G,∠FGC=2∠BAD,求证:BA平分∠FBE;
(3)如图3,在(2)的条件下,MN与⊙O相切于点M,交EB的延长线于点N,连接AM,若2∠MAD+∠FBA=135°,MN=![]() AB,EN=26,求线段CD的长.
AB,EN=26,求线段CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com