
”¾ĢāÄæ”æČēĶ¼£¬A£¬B£¬C£¬DĖÄµć¶¼ŌŚOOÉĻ£¬»”AC£½»”BC£¬Į¬½ÓAB£¬CD”¢AD£¬”ĻADC£½45”ć£®
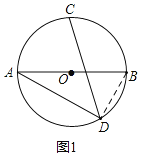
£Ø1£©ČēĶ¼1£¬ABŹĒ”ŃOµÄÖ±¾¶£»
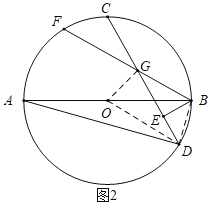
£Ø2£©ČēĶ¼2£¬¹żµćB×÷BE”ĶCDÓŚµćE£¬µćFŌŚ»”ACÉĻ£¬Į¬½ÓBF½»CDÓŚµćG£¬”ĻFGC£½2”ĻBAD£¬ĒóÖ¤£ŗBAĘ½·Ö”ĻFBE£»
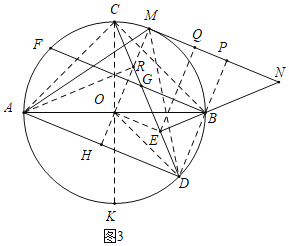
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬MNÓė”ŃOĻąĒŠÓŚµćM£¬½»EBµÄŃÓ³¤ĻßÓŚµćN£¬Į¬½ÓAM£¬Čō2”ĻMAD+”ĻFBA£½135”ć£¬MN£½![]() AB£¬EN£½26£¬ĒóĻ߶ĪCDµÄ³¤£®
AB£¬EN£½26£¬ĒóĻ߶ĪCDµÄ³¤£®

”¾“š°ø”æ£Ø1£©Ļź¼ū½āĪö£»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©34
”¾½āĪö”æ
(1)øł¾ŻÖ±¾¶Ėł¶ŌŌ²ÖܽĒŹĒÖ±½Ē¼“æɽāĢā;
(2)×÷øØÖśĻß,Ķعż°ė¾¶ĻąµČµĆµ½µČŃüČż½ĒŠĪ,ÓÉŅŃÖŖµÄ”ĻFGC£½2”ĻBADµĆµ½B”¢G”¢O”¢DĖÄµć¹²Ō²£¬ĶĘ³ö”ĻODE£½”ĻOBG¼“æɽāĢā;
(3)×÷øØÖśĻß,ĶعżÖ±¾¶Ėł¶ŌŌ²ÖܽĒŹĒÖ±½ĒµĆµ½”ĻACB£½90”ć,øł¾Ż2”ĻMAD+”ĻFBA£½135”ć£¬µĆµ½AM£½DM£¬½Ó×ÅÖ¤Ć÷”÷ADRŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”÷ACR”Õ”÷CBE£ØAAS£©£¬ĖıߊĪOEQMŹĒ¾ŲŠĪ£¬ŌŁ”÷EQNŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”÷OERŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬×īŗóĶعż¹“¹É¶ØĄķ¼“æɽāĢā.
½ā£Ø1£©ČēĶ¼1£¬Į¬½ÓBD£®
”ß![]() £¬
£¬
”ą”ĻBDC£½”ĻADC£½45”ć£¬
”ą”ĻADB£½90”ć£¬
”ąABŹĒŌ²OµÄÖ±¾¶£®
£Ø2£©ČēĶ¼2£¬Į¬½ÓOG”¢OD”¢BD£®
ŌņOA£½OD£½OB£¬
”ą”ĻOAD£½”ĻODA£¬”ĻOBD£½”ĻODB£¬
”ą”ĻDOB£½”ĻOAD+”ĻODA£½2”ĻBAD£¬
”ß”ĻFGC£½2”ĻBAD£¬
”ą”ĻDOB£½”ĻFGC£½”ĻBGD£¬
”ąB”¢G”¢O”¢DĖÄµć¹²Ō²£¬
”ą”ĻODE£½”ĻOBG£¬
”ßBE”ĶCD£¬”ĻBDC£½45”ć£¬
”ą”ĻEBD£½45”ć£½”ĻEDB£¬
”ą”ĻOBE£½”ĻODE£½”ĻOBG£¬
”ąBAĘ½·Ö”ĻFBE£®
£Ø3£©ČēĶ¼3£¬Į¬½ÓAC”¢BC”¢CO”¢DO”¢EO”¢BD£®
”ßAC£½BC£¬
”ąAC£½BC£¬
”ßABĪŖÖ±¾¶£¬
”ą”ĻACB£½90”ć£¬”ĻCAB£½”ĻCBA£½45”ć£¬CO”ĶAB£¬
ŃÓ³¤CO½»Ō²OÓŚµćK£¬Ōņ”ĻDOK£½”ĻOCD+”ĻODC£½2”ĻODC£½2”ĻOBE£½2”ĻFBA£¬
Į¬½ÓDM”¢OM£¬Ōņ”ĻMOD£½2”ĻMAD£¬
”ß2”ĻMAD+”ĻFBA£½135”ć£¬
”ą”ĻMOD+”ĻFBA£½135”ć£¬
”ą2”ĻMOD+2”ĻFBA£½270”ć£¬
”ą2”ĻMOD+”ĻDOK£½270”ć£¬
”ß”ĻAOM+”ĻDOM+”ĻKOK£½270”ć£¬
”ą”ĻAOM£½”ĻDOM£¬
”ąAM£½DM£¬
Į¬½ÓMO²¢ŃÓ³¤½»ADÓŚH£¬Ōņ”ĻMHA£½”ĻMHD£½90”ć£¬AH£½DH£¬
ÉčMHÓėBC½»ÓŚµćR£¬Į¬½ÓAR£¬ŌņAR£½DR£¬
”ß”ĻADC£½45”ć£¬
”ą”ĻARD£½”ĻARC£½90”ć£¬”÷ADRŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻBRH£½”ĻARH£½45”ć
”ß”ĻACR+”ĻBCE£½”ĻBCE+”ĻCBE£½90”ć£¬
”ą”ĻACR£½”ĻCBE£¬
”ą”÷ACR”Õ”÷CBE£ØAAS£©£¬
”ąCR£½BE£½ED£¬
×÷EQ”ĶMNÓŚQ£¬Ōņ”ĻEQN£½”ĻEQM£½90”ć£¬
Į¬½ÓOE£¬ŌņOE“¹Ö±Ę½·ÖBD£¬
”ąOE”ĪAD”ĪMN£¬
”ąĖıߊĪOEQMŹĒ¾ŲŠĪ£¬
”ąOM£½EQ£¬OE£½MQ£¬
ŃÓ³¤DB½»MNÓŚµćP£¬
”ß”ĻPBN£½”ĻEBD£½45”ć£¬
”ą”ĻBNP£½45”ć£¬
”ą”÷EQNŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąEQ£½QN£½![]() EN£½13
EN£½13![]() £¬
£¬
”ąOA£½OB£½OC£½OD£½OMØT13![]() £¬AB£½2OA£½26
£¬AB£½2OA£½26![]() £¬
£¬
”ąBC£½![]() OC£½26£¬
OC£½26£¬
”ßMN£½![]() AB£½20
AB£½20![]() £¬
£¬
”ąOE£½MQ£½MN©QN£½20![]() ©13
©13![]() £½7
£½7![]() £¬
£¬
”ß”ĻORE£½45”ć£¬”ĻEOR£½90”ć£¬
”ą”÷OERŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąRE£½![]() OE£½14£¬
OE£½14£¬
ÉčBE£½CR£½x£¬ŌņCE£½14+x£¬
ŌŚRt”÷CBEÖŠ£ŗBC2£½CE2+BE2£¬
”ą262£½£Øx+14£©2+x2£¬½āµĆx£½10£¬
”ąCD£½CR+RE+DE£½10+14+10£½34£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
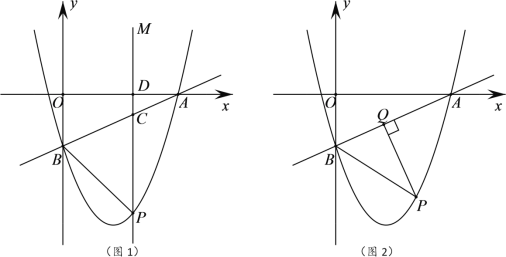
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼Ļń·Ö±š½»x”¢yÖįÓŚµćA”¢B£¬Å×ĪļĻß
µÄĶ¼Ļń·Ö±š½»x”¢yÖįÓŚµćA”¢B£¬Å×ĪļĻß![]() ¾¹żµćA”¢B£¬µćPĪŖµŚĖÄĻóĻŽÄŚÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć.
¾¹żµćA”¢B£¬µćPĪŖµŚĖÄĻóĻŽÄŚÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć.
£Ø1£©Ēó“ĖÅ×ĪļĻ߶ŌÓ¦µÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČēĶ¼1ĖłŹ¾£¬¹żµćP×÷PM”ĪyÖį£¬·Ö±š½»Ö±ĻßAB”¢xÖįÓŚµćC”¢D£¬ČōŅŌµćP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪÓėŅŌµćA”¢C”¢DĪŖ¶„µćµÄČż½ĒŠĪĻąĖĘ£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼2ĖłŹ¾£¬¹żµćP×÷PQ”ĶABÓŚµćQ£¬Į¬½ÓPB£¬µ±”÷PBQ֊ӊijøö½ĒµÄ¶ČŹżµČÓŚ”ĻOAB¶ČŹżµÄ2±¶Ź±£¬ĒėÖ±½ÓŠ“³öµćPµÄŗį×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() Ķā£¬Į¬½Ó
Ķā£¬Į¬½Ó![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £®
£®
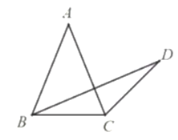
£Ø1£©Čō![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø2£©Čō![]() £¬Ēó
£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
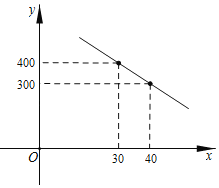
”¾ĢāÄæ”æijĶÆ×°µź¹ŗ½ųŅ»Åś20ŌŖ/¼žµÄĶÆ×°£¬ÓÉĻśŹŪ¾ŃéÖŖ£¬ĆæĢģµÄĻśŹŪĮæy£Ø¼ž£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼ä“ęŌŚČēĶ¼µÄŅ»“ĪŗÆŹż¹ŲĻµ£®
£Ø1£©ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£»
£Ø2£©µ±ĻśŹŪµ„¼Ū¶ØĪŖ¶ąÉŁŹ±£¬ĆæĢģæÉ»ńµĆ×ī“óĄūČó£¬×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2-x-£Øm+1£©=0ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®
£Ø1£©ĒómµÄȔֵ·¶Ī§£»
£Ø2£©ČōmĪŖ·ūŗĻĢõ¼žµÄ×īŠ”ÕūŹż£¬Ēó“Ė·½³ĢµÄøł£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóČēĶ¼£¬øų³öĻĀĮŠĖÄøö½įĀŪ£ŗ¢Ł4ac©b2£¼0£»¢Ś4a+c£¼2b£»¢Ū3b+2c£¼0£»¢Üm£Øam+b£©+b£¼a£Øm”Ł©1£©£¬ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©
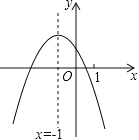
A.4øöB.3øöC.2øöD.1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖĘ½ŠŠĖıߊĪABCDµÄµćA£Ø0£¬©2£©”¢µćB£Ø3m£¬4m+1£©£Øm”Ł©1£©£¬µćC£Ø6£¬2£©£¬Ōņ¶Ō½ĒĻßBDµÄ×īŠ”ÖµŹĒ£Ø””””£©
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚµČ±ß![]() ÖŠ£¬
ÖŠ£¬![]() £¬¶Æµć
£¬¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŃŲ
³ö·¢£¬ŃŲ![]() ±ßŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÖÕµć
±ßŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÖÕµć![]() ŌĖ¶Æ£¬Ķ¬Ź±¶Æµć
ŌĖ¶Æ£¬Ķ¬Ź±¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ×Å
³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ×Å![]() ·½ĻņŌĖ¶Æ£®Į¬½į
·½ĻņŌĖ¶Æ£®Į¬½į![]() £¬Éčµć
£¬Éčµć![]() ŌĖ¶ÆµÄŹ±¼ä
ŌĖ¶ÆµÄŹ±¼ä![]() Ćė£®
Ćė£®
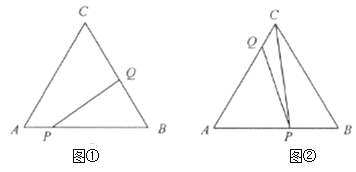
£Ø1£©ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾Ļ߶Ī
µÄ“śŹżŹ½±ķŹ¾Ļ߶Ī![]() µÄ³¤£®
µÄ³¤£®
£Ø2£©µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
£Ø3£©Čō![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©ČēĶ¼¢Ś£¬µ±µć![]() ŌŚ
ŌŚ![]() ”¢
”¢![]() Ö®¼äŹ±£¬Į¬½į
Ö®¼äŹ±£¬Į¬½į![]() £¬
£¬![]() ±»·Öøī³É
±»·Öøī³É![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬µ±ĘäÖŠµÄijĮ½øöČż½ĒŠĪĆ껿ĻąµČŹ±£¬Ö±½ÓŠ“³ö
£¬µ±ĘäÖŠµÄijĮ½øöČż½ĒŠĪĆ껿ĻąµČŹ±£¬Ö±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČżĆūæģµŻŌ±Ä³ĢģµÄ¹¤×÷ĒéæöČēĶ¼ĖłŹ¾£¬ĘäÖŠµć![]() £¬
£¬![]() £¬
£¬![]() µÄŗį”¢×Ż×ų±ź·Ö±š±ķŹ¾¼×”¢ŅŅ”¢±ūČżĆūæģµŻŌ±ÉĻĪēÅÉĖĶæģµŻĖłÓƵď±¼äŗĶ¼žŹż£»µć
µÄŗį”¢×Ż×ų±ź·Ö±š±ķŹ¾¼×”¢ŅŅ”¢±ūČżĆūæģµŻŌ±ÉĻĪēÅÉĖĶæģµŻĖłÓƵď±¼äŗĶ¼žŹż£»µć![]() £¬
£¬![]() £¬
£¬![]() £¬µÄŗį”¢×Ż×ų±ź·Ö±š±ķŹ¾¼×”¢ŅŅ”¢±ūČżĆūæģµŻŌ±ĻĀĪēÅÉĖĶæģµŻĖłÓƵď±¼äŗĶ¼žŹż.ÓŠČēĻĀČżøö½įĀŪ£ŗ¢ŁÉĻĪēÅÉĖĶæģµŻĖłÓĆŹ±¼ä×ī¶ĢµÄŹĒ¼×£»¢ŚĻĀĪēÅÉĖĶæģµŻ¼žŹż×ī¶ąµÄŹĒ±ū£»¢ŪŌŚÕāŅ»ĢģÖŠÅÉĖĶæģµŻ×ܼžŹż×ī¶ąµÄŹĒŅŅ.ÉĻŹö½įĀŪÖŠ£¬ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅŹĒ£Ø £©
£¬µÄŗį”¢×Ż×ų±ź·Ö±š±ķŹ¾¼×”¢ŅŅ”¢±ūČżĆūæģµŻŌ±ĻĀĪēÅÉĖĶæģµŻĖłÓƵď±¼äŗĶ¼žŹż.ÓŠČēĻĀČżøö½įĀŪ£ŗ¢ŁÉĻĪēÅÉĖĶæģµŻĖłÓĆŹ±¼ä×ī¶ĢµÄŹĒ¼×£»¢ŚĻĀĪēÅÉĖĶæģµŻ¼žŹż×ī¶ąµÄŹĒ±ū£»¢ŪŌŚÕāŅ»ĢģÖŠÅÉĖĶæģµŻ×ܼžŹż×ī¶ąµÄŹĒŅŅ.ÉĻŹö½įĀŪÖŠ£¬ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅŹĒ£Ø £©
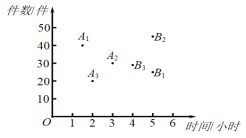
A. ¢Ł¢ŚB. ¢Ł¢ŪC. ¢ŚD. ¢Ś¢Ū
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com