
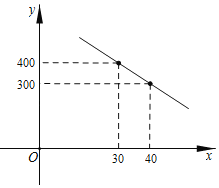
【题目】某童装店购进一批20元/件的童装,由销售经验知,每天的销售量y(件)与销售单价x(元)之间存在如图的一次函数关系.
(1)求y与x之间的函数关系;
(2)当销售单价定为多少时,每天可获得最大利润,最大利润是多少?
【答案】(1)y=﹣10x+700;(2)销售单价为45元时,每天可获得最大利润,最大利润为6250元
【解析】
(1)由一次函数的图象可知过(30,400)和(40,300),利用待定系数法可求得y与x的关系式;
(2)利用x可表示出p,再利用二次函数的性质可求得p的最大值.
(1)设一次函数解析式为y=kx+b(k≠0),
由图象可知一次函数的过(30,400)和(40,300),
代入解析式可得![]() ,
,
解得:![]() ,
,
∴y与x的函数关系式为y=﹣10x+700;
(2)设利润为p元,由(1)可知每天的销售量为y千克,
∴p=y(x﹣20)=(﹣10x+700)(x﹣20)=﹣10x2+900x﹣14000=﹣10(x﹣45)2+6250.
∵﹣10<0,
∴p=﹣10(x﹣45)2+6250是开口向下的抛物线,
∴当x=45时,p有最大值,最大值为6250元,
即销售单价为45元时,每天可获得最大利润,最大利润为6250元.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
![]()
A. ﹣74 B. ﹣77 C. ﹣80 D .﹣83
查看答案和解析>>
科目:初中数学 来源: 题型:
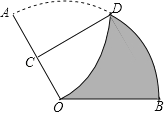
【题目】如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
A.9![]() B.12π﹣9
B.12π﹣9![]() C.
C.![]() D.6π﹣
D.6π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=![]() 在第一象限内的图象与△ABC有交点,则k的取值范围是_____.
在第一象限内的图象与△ABC有交点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D四点都在OO上,弧AC=弧BC,连接AB,CD、AD,∠ADC=45°.
(1)如图1,AB是⊙O的直径;
(2)如图2,过点B作BE⊥CD于点E,点F在弧AC上,连接BF交CD于点G,∠FGC=2∠BAD,求证:BA平分∠FBE;
(3)如图3,在(2)的条件下,MN与⊙O相切于点M,交EB的延长线于点N,连接AM,若2∠MAD+∠FBA=135°,MN=![]() AB,EN=26,求线段CD的长.
AB,EN=26,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
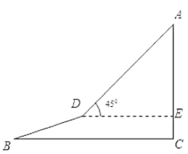
【题目】如图,一勘测人员从山脚![]() 点出发,沿坡度为
点出发,沿坡度为![]() 的坡面
的坡面![]() 行至
行至![]() 点处时,他的垂直高度上升了
点处时,他的垂直高度上升了![]() 米;然后再从
米;然后再从![]() 点处沿坡角为
点处沿坡角为![]() 的坡面
的坡面![]() 以
以![]() 米/分钟的速度到达山顶
米/分钟的速度到达山顶![]() 点时,用了
点时,用了![]() 分钟.
分钟.
(1)求![]() 点到
点到![]() 点之间的水平距离;
点之间的水平距离;
(2)求山顶![]() 点处的垂直高度
点处的垂直高度![]() 是多少米?(
是多少米?(![]() 结果保留整数)
结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com