
【题目】如图①,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 边以每秒1个单位的速度向终点
边以每秒1个单位的速度向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿着
出发,以每秒2个单位的速度沿着![]() 方向运动.连结
方向运动.连结![]() ,设点
,设点![]() 运动的时间
运动的时间![]() 秒.
秒.
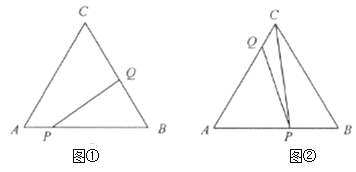
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)若![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)如图②,当点![]() 在
在![]() 、
、![]() 之间时,连结
之间时,连结![]() ,
,![]() 被分割成
被分割成![]() 、
、![]() 、
、![]() ,当其中的某两个三角形面积相等时,直接写出
,当其中的某两个三角形面积相等时,直接写出![]() 的值.
的值.
【答案】(1)当0≤![]() ≤3时,
≤3时,![]() ,当3<
,当3<![]() ≤6时,
≤6时,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() 或
或![]()
【解析】
(1)分类讨论:当0≤![]() ≤3时和当3<
≤3时和当3<![]() ≤6时,根据题目意思结合图形解答即可;
≤6时,根据题目意思结合图形解答即可;
(2)根据直角三角形的性质列出方程,解方程得到答案;
(3)作QH⊥AB于H,根据直角三角形的性质用t表示出QH,根据三角形的面积公式解答;
(4)分△APQ的面积=△PCQ的面积、△APQ的面积=△PCB的面积、△CPQ的面积=△PCB的面积三种情况进行讨论.
解:(1)由题意知得:点Q的运动路程为2t,
当0≤![]() ≤3时,
≤3时,![]() ,
,
当3<![]() ≤6时,
≤6时,![]() .
.
(2)∵△ABC为等边三角形,
∴∠A=60°,
当![]() 时,∠QPA=30°,
时,∠QPA=30°,
∴AQ=![]() ,即
,即![]() ,
,
解得![]() .
.
(3)如图①所示,作QH⊥AB于H,

在Rt△QBH中,![]() ,
,
![]() ,
,
如图②所示,作QH⊥AB于H,
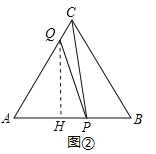
在Rt△QAH中,![]() ,
,
![]() .
.
(4)当点Q为AC的中点时,△APQ的面积=△PCQ的面积,
即12-2t=3,
解得:![]() ,
,
如图①,作CE⊥AB于E,
则![]() ,
,
∴△ABC的面积:![]() ,
,
![]() ,
,
∴△BPC的面积:![]() ,
,
∴△APC的面积:![]() ,
,
![]() ,
,
∴△APQ的面积:![]() ,
,
∴△APC的面积:![]() ,
,
当△APQ的面积=△PCB的面积时,
![]() ,
,
整理得:t2-t+4=0,
△=1-16=-15<0,此方程无解,
当△CPQ的面积=△PCB的面积时,
![]() ,
,
解得:![]() (舍去),
(舍去),
综上所述:在△APQ、△PCQ、△PBC中,其中某两个三角形相等时,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D四点都在OO上,弧AC=弧BC,连接AB,CD、AD,∠ADC=45°.
(1)如图1,AB是⊙O的直径;
(2)如图2,过点B作BE⊥CD于点E,点F在弧AC上,连接BF交CD于点G,∠FGC=2∠BAD,求证:BA平分∠FBE;
(3)如图3,在(2)的条件下,MN与⊙O相切于点M,交EB的延长线于点N,连接AM,若2∠MAD+∠FBA=135°,MN=![]() AB,EN=26,求线段CD的长.
AB,EN=26,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
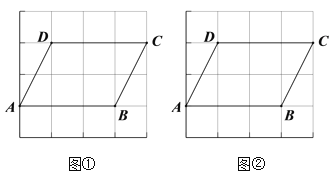
【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的![]() .(保留作图痕迹)
.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
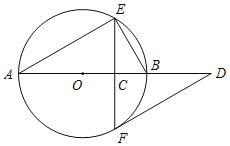
【题目】如图,AB是⊙O的直径,弦EF⊥AB于点C,过点F作⊙O的切线交AB的延长线于点D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中点M,连接MF,请补全图形;若∠A=30°,MF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
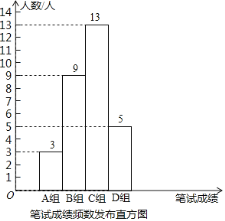
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
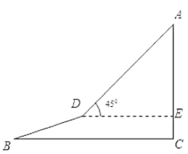
【题目】如图,一勘测人员从山脚![]() 点出发,沿坡度为
点出发,沿坡度为![]() 的坡面
的坡面![]() 行至
行至![]() 点处时,他的垂直高度上升了
点处时,他的垂直高度上升了![]() 米;然后再从
米;然后再从![]() 点处沿坡角为
点处沿坡角为![]() 的坡面
的坡面![]() 以
以![]() 米/分钟的速度到达山顶
米/分钟的速度到达山顶![]() 点时,用了
点时,用了![]() 分钟.
分钟.
(1)求![]() 点到
点到![]() 点之间的水平距离;
点之间的水平距离;
(2)求山顶![]() 点处的垂直高度
点处的垂直高度![]() 是多少米?(
是多少米?(![]() 结果保留整数)
结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),二次函数![]() 的图象与
的图象与![]() 轴、直线
轴、直线![]() 的交点分别为点
的交点分别为点![]() 、
、![]() .
.

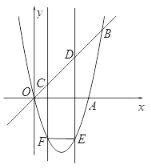

图(1) 图(2) (备用图)
(1)![]()
![]() _________,
_________,![]()
![]() _________,
_________,![]() =_________
=_________![]() ;
;
(2)连接AB,点![]() 是抛物线上一点(异于点A),且
是抛物线上一点(异于点A),且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图(2),点![]() 、
、![]() 是线段
是线段![]() 上的动点,且
上的动点,且![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
①过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线相交于点
轴的垂线,与抛物线相交于点![]() 、
、![]() ,连接
,连接![]() .当
.当![]() 取得最大值时,求
取得最大值时,求![]() 的值并判断四边形
的值并判断四边形![]() 的形状;
的形状;
②连接![]() 、
、![]() ,求
,求![]() 为何值时,
为何值时,![]() 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com