
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 外,连接
外,连接![]() ,
,![]() ,且
,且![]() .
.
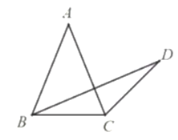
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,根据等腰三角形的性质,可设
,根据等腰三角形的性质,可设![]() ,设
,设![]() ,根据三角形外角的性质以及三角形的内角和可得出∠BCD=90°+y,再由
,根据三角形外角的性质以及三角形的内角和可得出∠BCD=90°+y,再由![]() 列方程即可求出y的值,从而得出结果;
列方程即可求出y的值,从而得出结果;
(2)解法一:过点![]() 作
作![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() 作
作![]() ,证明
,证明![]() ,再结合相似三角形的性质可得出结果;解法二:如图,过点
,再结合相似三角形的性质可得出结果;解法二:如图,过点![]() 作
作![]() 交于点
交于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .证明
.证明![]() ,再结合相似三角形的性质可得出结果;解法三:将
,再结合相似三角形的性质可得出结果;解法三:将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() .先证明
.先证明![]() 为等腰直角三角形,再证明
为等腰直角三角形,再证明![]() ,结合相似三角形的性质可得出结果.
,结合相似三角形的性质可得出结果.
解:(1)如图,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,
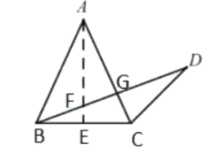
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴设![]() ,
,
∴![]() ,
,
设![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 的度数为
的度数为![]() .
.
(2)解法一:如图,过点![]() 作
作![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() 作
作![]() ,
,
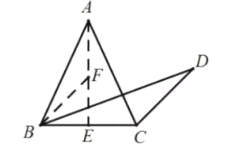
则∠FBE=∠EBF=45°,△BEF为等腰直角三角形.
∵AB=AC,∴BE=CE.
∵![]() ,∴
,∴![]() ,
,
又![]() ,∠AFB+∠BFE=180°,∠ABD=∠BFE=45°,
,∠AFB+∠BFE=180°,∠ABD=∠BFE=45°,
∴![]() ,
,
∴![]() ,
,
故![]() ,即
,即![]() .
.
解法二:如图,过点![]() 作
作![]() 交于点
交于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
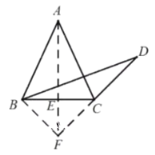
∵![]() 且
且![]() ,∴
,∴![]() ,
,
∴![]() ,∴∠ECF=∠EFC=45°,∴
,∴∠ECF=∠EFC=45°,∴![]() ,
,
又![]() ,则
,则![]() ,
,
故![]() 且
且![]() ,
,
∴∠ABD=∠EBF,
∴![]() .
.
∴![]() ,
,
∴![]() ,即
,即![]() .
.
解法三:如图,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() .
.
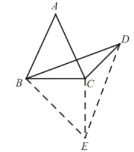
∵![]() 且
且![]() ,∴
,∴![]() =∠DCE,
=∠DCE,
∴![]() ,又
,又![]() ,即
,即![]() 为等腰直角三角形.
为等腰直角三角形.
∴∠CBE=∠ABD=45°,∴∠ABC=∠DBE,
又![]() ,
,![]() ,
,
∴∠ACB=∠DEB,
∴![]() ,
,
∴![]() ,故
,故![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图像如图所示.

(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() 在
在![]() 轴上,以点
轴上,以点![]() 为直角顶点作等腰直角
为直角顶点作等腰直角![]() ..当点
..当点![]() 落在某函数的图象上时,称点
落在某函数的图象上时,称点![]() 为该函数的“悬垂点”,
为该函数的“悬垂点”,![]() 为该函数的“悬垂等腰直角三角形”.
为该函数的“悬垂等腰直角三角形”.
(1)若点![]() 是函数
是函数![]() 的悬垂点,直接写出点
的悬垂点,直接写出点![]() 的横坐标为________.
的横坐标为________.
(2)若反比例函数![]()
![]() 的悬垂等腰直角三角形面积是
的悬垂等腰直角三角形面积是![]() ,求
,求![]() 的值.
的值.
(3)对于函数![]() ,当
,当![]()
![]() 时,该函数的悬垂点只有一个,求
时,该函数的悬垂点只有一个,求![]() 的取值范围.
的取值范围.
(4)若函数![]() 的悬垂等腰直角
的悬垂等腰直角![]() 的面积范围为
的面积范围为![]() ,且点
,且点![]() 在第一象限,直接写出
在第一象限,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°和106°,由此可知三角板的较短直角边的长度为 cm.(参考数据:tan37°=0.75)
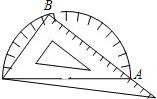
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
![]()
A. ﹣74 B. ﹣77 C. ﹣80 D .﹣83
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
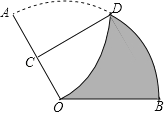
A.9![]() B.12π﹣9
B.12π﹣9![]() C.
C.![]() D.6π﹣
D.6π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D四点都在OO上,弧AC=弧BC,连接AB,CD、AD,∠ADC=45°.
(1)如图1,AB是⊙O的直径;
(2)如图2,过点B作BE⊥CD于点E,点F在弧AC上,连接BF交CD于点G,∠FGC=2∠BAD,求证:BA平分∠FBE;
(3)如图3,在(2)的条件下,MN与⊙O相切于点M,交EB的延长线于点N,连接AM,若2∠MAD+∠FBA=135°,MN=![]() AB,EN=26,求线段CD的长.
AB,EN=26,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
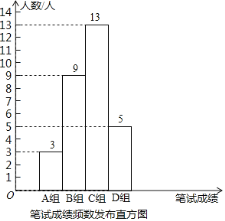
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com