
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() .
.
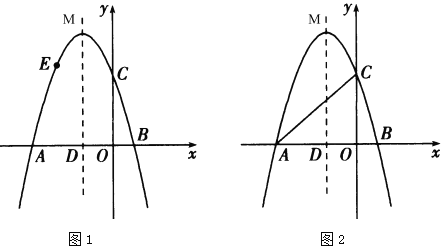
(1)求抛物线的表达式和顶点![]() 的坐标;
的坐标;
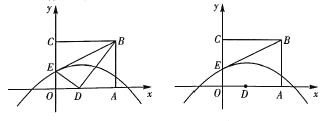
(2)如图1,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合,当
重合,当![]() 时,过点
时,过点![]() 作
作![]() 轴,交抛物线的对称轴于点
轴,交抛物线的对称轴于点![]() ,作
,作![]() 轴于点H,得到矩形
轴于点H,得到矩形![]() ,求矩形
,求矩形![]() 的周长的最大值;
的周长的最大值;
(3)如图2,点![]() 为抛物线对称轴上一点,是否存在点
为抛物线对称轴上一点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形?若存在,求出点
为顶点的三角形是直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,顶点坐标
,顶点坐标![]() ;(2)周长的最大值为
;(2)周长的最大值为![]() ;(3)存在,P的坐标为
;(3)存在,P的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)把A、B坐标代入y=-x2+bx+c,解方程组求出b、c的值即可得答案;(2)设矩形![]() 的周长为
的周长为![]() ,
,![]() ,分别讨论-7<x<-3时和-3<x<-2时两种情况,用x表示出矩形的周长,根据二次函数的性质求出最大值即可得答案;(3)设
,分别讨论-7<x<-3时和-3<x<-2时两种情况,用x表示出矩形的周长,根据二次函数的性质求出最大值即可得答案;(3)设![]() 分
分![]() 时,
时,![]() 时,
时,![]() 时,三种情况讨论,利用勾股定理求出m的值即可得答案.
时,三种情况讨论,利用勾股定理求出m的值即可得答案.
(1)把![]() 两点坐标代入
两点坐标代入![]()
得![]() ,
,
解得:![]() ,
,
∴抛物线方程为:![]() ,顶点坐标
,顶点坐标![]() ,
,
(2)
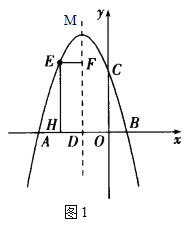
如图1,设矩形![]() 的周长为
的周长为![]() ,
,![]() ,
,
∴![]() ,
,
∵A(-7,0),B(1,0),
∴抛物线对称轴为直线x=-3,
①当![]() 时,
时,
![]() ,
,
![]() ,
,
=![]()
=![]()
=![]()
=![]()
![]()
∵![]() ,
,
∴![]() 时,矩形周长最大,最大值为
时,矩形周长最大,最大值为![]() .
.
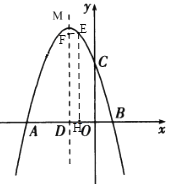
②当![]() 时
时
EF=x-(-3)=x+3,
l=![]()
=![]()
![]() .
.
∴当![]() 时,矩形周长最大,最大值为
时,矩形周长最大,最大值为![]()
∴综上所述,周长的最大值为![]()
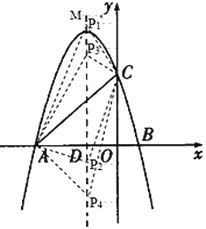
(3)存在.如下图
设![]()
(i)当![]() 时,
时,![]()
16+![]()
16![]()
2![]()
m2![]()
解得:![]()
∴P1![]() ,P2
,P2![]()
(ii)当![]() 时,
时,![]()
49+49+9+(7-m)2=16+m2
∴![]()
140=14m,
m=10,
∴P3![]() ,
,
(iii)当![]() 时,
时,![]()
98+16+m2=9+(7-m)2
49+49+16+m2=9+49-14m+m2
56=-14m
解得:![]() ,
,
∴P4![]()
综上所述:满足条件的点P的坐标为![]() ,
,![]() ,
,![]() ,
,![]()


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
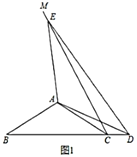
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
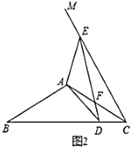
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 交于点
交于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有2个相同的小球,它们分别写有数值![]() ;乙口袋中装有3个相同的小球,它们分别写有数值
;乙口袋中装有3个相同的小球,它们分别写有数值![]() .现从甲口袋中随机取一球,记它上面的数值为
.现从甲口袋中随机取一球,记它上面的数值为![]() ,再从乙口袋中随机取一球,记它上面的数值为
,再从乙口袋中随机取一球,记它上面的数值为![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)请用树状图或列表法,列出![]() 所有可能的结果;
所有可能的结果;
(2)求点![]() 落在第一象限的概率.
落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):
温度 | …… |
|
| 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是一次函数和二次函数中的一种.
的函数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外一种函数的理由;
(2)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过![]() ,那么实验室的温度
,那么实验室的温度![]() 应该在哪个范围内选择?请说明理由.
应该在哪个范围内选择?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
![]()
A. ﹣74 B. ﹣77 C. ﹣80 D .﹣83
查看答案和解析>>
科目:初中数学 来源: 题型:
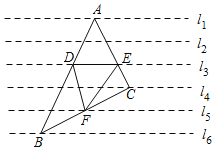
【题目】如图,一组等距的平行线,点A、B、C分别在直线l1、l6、l4上,AB交l3于点D,AC交l3于点E,BC交于l5点F,若△DEF的面积为1,则△ABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=![]() 在第一象限内的图象与△ABC有交点,则k的取值范围是_____.
在第一象限内的图象与△ABC有交点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
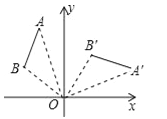
A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若折叠矩形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,已知折痕
处,已知折痕![]() 且.以
且.以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立如图所示的平面直角坐标系,抛物线
轴建立如图所示的平面直角坐标系,抛物线![]() 经过点
经过点![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 是线段
是线段![]() 上一动点,点
上一动点,点![]() 在抛物线上,且始终满足
在抛物线上,且始终满足![]() ,在点
,在点![]() 运动过程中,能否使得
运动过程中,能否使得![]() ?若能,求出所有符合条件的点
?若能,求出所有符合条件的点![]() 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)已知点![]() 是拋物线上一动点,点
是拋物线上一动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,若在
,若在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 有最小值,求点
有最小值,求点![]() 的纵坐标的最大值.
的纵坐标的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com