
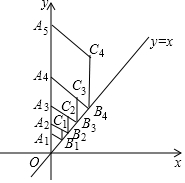
 如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].
如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016]. 分析 求出A1~A4的坐标,探究规律后,利用规律解决问题即可.
解答 解:∵点A1的坐标为(0,1),
∴OA1=1,
在Rt△A1B1O中,A1B1=$\frac{\sqrt{2}}{2}$OA1=$\frac{\sqrt{2}}{2}$,
∴A2[0,(1+$\frac{\sqrt{2}}{2}$),
同法可得A2B2=$\frac{\sqrt{2}}{2}$OA2=$\frac{\sqrt{2}}{2}$(1+$\frac{\sqrt{2}}{2}$),
∴OA3=(1+$\frac{\sqrt{2}}{2}$)(1+$\frac{\sqrt{2}}{2}$)=(1+$\frac{\sqrt{2}}{2}$)2,
∴A3[0,(1+$\frac{\sqrt{2}}{2}$)2],
同法可得OA4=(1+$\frac{\sqrt{2}}{2}$)3,
∴A4[0,(1+$\frac{\sqrt{2}}{2}$)3],
…,
A2017[0,(1+$\frac{\sqrt{2}}{2}$)2016].
故答案为[0,(1+$\frac{\sqrt{2}}{2}$)2016].
点评 本题考查菱形的性质、规律型-点的坐标.等腰直角三角形的性质等知识,解题的关键是学会从特殊到一般的探究方法,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
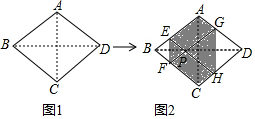 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在菱形ABCD中,AB=5,AC=8,点P是AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在点A'处,当△A'CD
在菱形ABCD中,AB=5,AC=8,点P是AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在点A'处,当△A'CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | b | 1 | 0 | 1 | 2 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com