
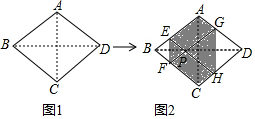
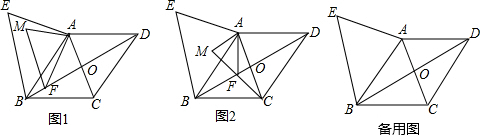
 ��ͼ1������ֽƬABCD�ı߳�Ϊ2����ABC=60�㣬���ۡ�B����D��ʹ��B��D�����غ��ڶԽ���BD��һ��P��EF��GH�ֱ����ۺۣ���ͼ2������AE=x��0��x��2�������������жϣ�
��ͼ1������ֽƬABCD�ı߳�Ϊ2����ABC=60�㣬���ۡ�B����D��ʹ��B��D�����غ��ڶԽ���BD��һ��P��EF��GH�ֱ����ۺۣ���ͼ2������AE=x��0��x��2�������������жϣ����� ��ȷ������ABC�ǵȱ������Σ������жϳ���BEF�ǵȱ������Σ���x=1ʱ�����BP=$\frac{1}{2}$BD�������жϳ�����ȷ������x��ʾ��EF��BP��DP��GH��Ȼ��ȡx�����ֵ���������EF��GH���жϳ��ڴ����������ε������ȥ���������ε�����жϳ��۴��������ܳ��ļ��㷽�������ж�������ȷ��
��� �⣺������ABCD�ı߳�Ϊ2��
��AB=BC=2��
�ߡ�ABC=60�㣬
��AC=AB=2��BD=2$\sqrt{3}$��
���۵�֪����BEF�ǵȱ������Σ�
��x=1ʱ����AE=1��
��BE=AB-AE=1��
���۵�֪��BP=2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$=$\frac{1}{2}$BD��
���P������ABCD�ĶԽ��ߵĽ��㣬
������P������ABCD�����ģ����Ԣ���ȷ��
��ͼ��
��AE=x��
��BE=AB-AE=2-x��
�ߡ�BEF�ǵȱ������Σ�
��EF=BE=2-x��
��BM=$\sqrt{3}$EM=$\sqrt{3}$��$\frac{1}{2}$EF=$\frac{\sqrt{3}}{2}$��2-x����
��BP=2BM=$\sqrt{3}$��2-x����
��DP=BD-BP=2$\sqrt{3}$-$\sqrt{3}$��2-x��=$\sqrt{3}$x��
��DN=$\frac{1}{2}$DP=$\frac{\sqrt{3}}{2}$x��
��GH=2GN=2��$\frac{1}{2}$x=x��
��x=$\frac{1}{2}$ʱ��AE=$\frac{1}{2}$��
��BE=AB-AE=$\frac{3}{2}$��
�ߡ�BEF�ǵȱ������Σ�
��EF=BE=$\frac{3}{2}$��BP=$\frac{3\sqrt{3}}{2}$��
��DP=$\frac{\sqrt{3}}{2}$��
��GH=DG=$\frac{1}{2}$��
��EF+GH=2=AC�����Ԣڴ���
��0��x��2ʱ��
��AE=x��
��BE=2-x��
��EF=2-x��
��BP=$\sqrt{3}$��2-x����
��DP=$\sqrt{3}$x��
��GH=2��$\frac{x}{2}$=x=DG=DH��
��������AEFCHG���=S����ABCD-S��BEEF-S��DGH
=$\frac{1}{2}$��2��2$\sqrt{3}$-$\frac{\sqrt{3}}{4}$��2-x��2-$\frac{\sqrt{3}}{4}$x2
=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$��x-1��2-$\frac{\sqrt{3}}{2}$
=-$\frac{\sqrt{3}}{2}$��x-1��2+$\frac{3\sqrt{3}}{2}$��
�൱x=1ʱ��������AEFCHG������Ϊ$\frac{3\sqrt{3}}{2}$�����Ԣ۴���
������AEFCHG�ܳ�=AE+EF+FC+CH+HG+AG
=x+2-x+x+2-x+x+2-x=6�Ƕ�ֵ��
���Ԣ���ȷ��������ȷ���Т٢ܣ�
�ʴ�Ϊ�٢ܣ�
���� �������ı��ε��ۺ��⣬��Ҫ���������ε����ʣ��ȱ������ε��ж������ʣ������ε������ʽ�����ε������ʽ���Ȿ��Ĺؼ�����x��ʾ����ص��߶Σ���һ��������Ŀ��


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y3��y1��y2 | B�� | y1��y2��y3 | C�� | y2��y1��y3 | D�� | y3��y2��y1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
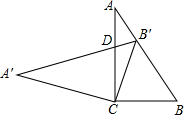 ��Rt��ABC�У���C=90�㣬cosB=0.6�������ֱ���������ƶ���C��ת��õ�Rt��A'B'C�����е�B'��������AB�ϣ�A'B'��AC�ཻ�ڵ�D����ôB��D��CD=0.35��
��Rt��ABC�У���C=90�㣬cosB=0.6�������ֱ���������ƶ���C��ת��õ�Rt��A'B'C�����е�B'��������AB�ϣ�A'B'��AC�ཻ�ڵ�D����ôB��D��CD=0.35���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
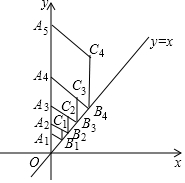 ��ͼ����ƽ��ֱ������ϵ�У���A1������Ϊ��0��1��������A1��ֱ��y=x�Ĵ��ߣ�����Ϊ��B1����A1B1Ϊ��������A1B2C2A3��ʹ�õ�A2����y���ϣ��ӳ�A2C1��ֱ���ڵ�B2������A2B2Ϊ��������A2B2C2A3��ʹ�õ�A3����y���ϡ������������������Σ����A2017��������[0����1+$\frac{\sqrt{2}}{2}$��2016]��
��ͼ����ƽ��ֱ������ϵ�У���A1������Ϊ��0��1��������A1��ֱ��y=x�Ĵ��ߣ�����Ϊ��B1����A1B1Ϊ��������A1B2C2A3��ʹ�õ�A2����y���ϣ��ӳ�A2C1��ֱ���ڵ�B2������A2B2Ϊ��������A2B2C2A3��ʹ�õ�A3����y���ϡ������������������Σ����A2017��������[0����1+$\frac{\sqrt{2}}{2}$��2016]���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
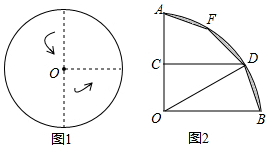 ��ͼ1����һԲ��ֽƬ���ҡ��������ζ��ۺ�õ���ͼ2��ʾ������AOB����֪OA=6��ȡOA���е�C������C��CD��OA��$\widehat{AB}$�ڵ�D����F��$\widehat{AB}$��һ�㣮��������BOD��OD���ۣ���Bǡ�����F�غϣ��ü��������߶�BD��DF��FA���μ��£�����µ�ֽƬ����״ͬ��Ӱͼ�Σ����֮��Ϊ36��-108��
��ͼ1����һԲ��ֽƬ���ҡ��������ζ��ۺ�õ���ͼ2��ʾ������AOB����֪OA=6��ȡOA���е�C������C��CD��OA��$\widehat{AB}$�ڵ�D����F��$\widehat{AB}$��һ�㣮��������BOD��OD���ۣ���Bǡ�����F�غϣ��ü��������߶�BD��DF��FA���μ��£�����µ�ֽƬ����״ͬ��Ӱͼ�Σ����֮��Ϊ36��-108���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 2.8 | C�� | 2 | D�� | $\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
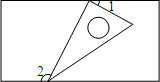 ��ͼ��һ������30��ǵ�ֱ�����ǰ�������������һ�����εĶԱ��ϣ������1=20�㣬��ô��2�Ķ����ǣ�������
��ͼ��һ������30��ǵ�ֱ�����ǰ�������������һ�����εĶԱ��ϣ������1=20�㣬��ô��2�Ķ����ǣ�������| A�� | 100�� | B�� | 105�� | C�� | 110�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=10��BD=24��E��AD���е㣬����OE�����߶�OE�ij����ڣ�������
��ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=10��BD=24��E��AD���е㣬����OE�����߶�OE�ij����ڣ�������| A�� | 5 | B�� | 13 | C�� | 6.5 | D�� | $\frac{60}{13}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com