
分析 (1)根据甲、乙两队每小时挖土量,进而利用每天需挖土700立方米,得出等式求出答案;
(2)分别求出甲、乙两队每挖土1立方米的费用,再利用每天最多挖土费用不超过14740元得出不等式进而求出答案;
(3)利用至少与最多的意义分析得出答案.
解答 解:(1)设甲、乙两队同时挖土,每天需x小时,根据题意可得:
(55+45)x=700,
解得:x=7,
答:甲、乙两队同时挖土,每天需7小时;
(2)∵甲队每小时挖土55立方米,需要费用1100元,乙队每小时挖土45立方米,需要费用990元,
∴甲队每挖土1立方米的费用是1100÷55=20(元),乙队每挖土1立方米的费用是990÷45=22(元),
设甲队每天挖土x立方米,则20x+22(700-x)≤14740,
解得:x≥330,
答:甲队每天至少挖土330立方米;
(3)∵乙队每挖土1立方米的费用高,
∴不能改问乙队每天至少挖土多少立方米,可以问乙队每天最多挖土多少立方米.
点评 此题主要考查了一元一次方程的应用以及一元一次不等式的应用,根据题意得出正确不等关系是解题关键.


科目:初中数学 来源: 题型:填空题
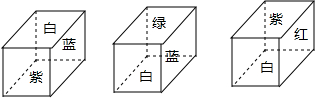 一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.
一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com