
分析 连接OB、OC,作OD⊥BC于D,则∠ODB=90°,由垂径定理得出BD=CD=$\frac{1}{2}$BC,由等腰三角形的性质得出∠BOD=∠COD=$\frac{1}{2}$∠BOC,由三角函数求出∠BOD=60°,得出∠BOC=120°,由圆周角定理即可得出结果.
解答 解:分两种情况: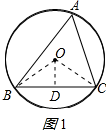
①当△ABC是锐角三角形时;连接OB、OC,作OD⊥BC于D,如图1所示:
则∠ODB=90°,BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$cm,∠BOD=∠COD=$\frac{1}{2}$∠BOC,
∵sin∠BOD=$\frac{BD}{OB}$,
∴∠BOD=60°,
∴∠BOC=120°,
∴∠A=$\frac{1}{2}$∠BOC=60°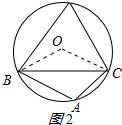
②当△ABC是钝角三角形时,如图2所示:
∠A=180°-60°=120°;
综上所述:∠A的度数为60°或120°,
故答案为:60°或120°.
点评 本题考查了三角形的外接圆、垂径定理、等腰三角形的性质、圆周角定理、三角函数等知识;本题综合性强,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①④ | C. | ②③④ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
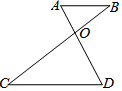 如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )| A. | 200 cm2 | B. | 300 cm2 | C. | 400 cm2 | D. | 500 cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该事件是必然事件 | B. | 该事件是不可能事件 | ||
| C. | 该事件是不确定事件 | D. | 该事件发生的可能性很大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com