
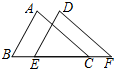
 已知:如图,E、C是BF上两点,且AB∥DE,BE=FC,∠A=∠D.求证:AC=DF.
已知:如图,E、C是BF上两点,且AB∥DE,BE=FC,∠A=∠D.求证:AC=DF. 分析 先根据平行线的性质得∠B=∠DEF,再由BE=FC得到BC=EF,则可根据“AAS”判断△ABC≌△DEF,然后根据全等三角形的性质即可得到AC=DF.
解答 证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=FC,
∴BE+EC=EC+CF,即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{A=∠D}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴AC=DF.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形;在应用全等三角形的性质时主要是得到对应角相等或对应线段相等.


科目:初中数学 来源: 题型:选择题
| A. | 任意掷一枚均匀的硬币,正面朝上 | B. | 篮球运动员投篮,投进篮筐 | ||
| C. | 一个星期有七天 | D. | 打开电视机,正在播放新闻 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
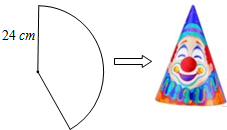 小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )| A. | 120πcm2 | B. | 240πcm2 | C. | 260πcm2 | D. | 480πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com