
【题目】如图,学校环保社成员想测量斜坡 ![]() 旁一棵树
旁一棵树 ![]() 的高度,他们先在点
的高度,他们先在点 ![]() 处测得树顶
处测得树顶 ![]() 的仰角为
的仰角为 ![]() ,然后在坡顶
,然后在坡顶 ![]() 测得树顶
测得树顶 ![]() 的仰角为
的仰角为 ![]() ,已知斜坡
,已知斜坡 ![]() 的长度为
的长度为 ![]() ,
, ![]() 的长为
的长为 ![]() ,则树
,则树 ![]() 的高度是( )
的高度是( ) ![]()
A.![]()
B.30
C.![]()
D.40
【答案】B
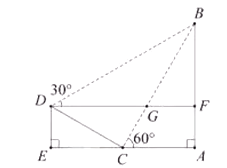
【解析】解:在Rt△DEC中,
∵CD=20,DE=10.
∴ ∠DCE=30°,∠CDE=60°.
∴ ∠CDF=30°.
又∵∠BDF=30°.∠BCA=60°.
∴ ∠BCD=30°.∠BDC=60°.
在Rt△BCD中,
∴ tan60°=![]() .
.
∴ BC=DCtan60°=20![]() .
.
在Rt△BAC中,
∴ sin60°=![]() .
.
∴ BA=BCsin60°=20![]() ×
×![]() =30(m).
=30(m).
故AB的高度为30m.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
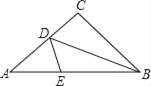
【题目】如图,三角形纸牌中,AB=8cm,BC=6cm,AC=5cm,沿着过△ABC的顶点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
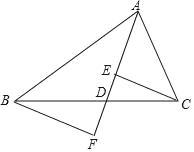
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法中正确的个数是( )
①CE=BF;②△ABD和△ADC的面积相等;③BF∥CE;④CE,BF均与AD垂直
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:
① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条直线都与第三条直线相交,∠1和∠2是内错角,∠3和∠2是邻补角.
(1)根据上述条件,画出符合题意的图形;
(2)若∠1∶∠2∶∠3=1∶2∶3,求∠1,∠2,∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.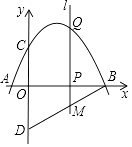
(1)求抛物线的解析式;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,是否存在点P,使得四边形CQMD是平行四边形?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com