
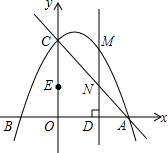
 ��ͼ��������y=-$\frac{1}{2}{x}^{2}+bx+c$����A��4��0����C��0��4�����㣬��B����������x�����һ�����㣬��E��OC���е㣬��ֱ��AC����M���������ϣ�����M��MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N�����M�ĺ�����Ϊm��MN�ij���Ϊd��
��ͼ��������y=-$\frac{1}{2}{x}^{2}+bx+c$����A��4��0����C��0��4�����㣬��B����������x�����һ�����㣬��E��OC���е㣬��ֱ��AC����M���������ϣ�����M��MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N�����M�ĺ�����Ϊm��MN�ij���Ϊd������ ��1�����ݴ���ϵ�������ɵ�ֱ�ߵĽ���ʽ��
��2�����ݴ���ϵ�������ɵ������ߵĽ���ʽ��
��3������ƽ����y���ֱ���������ľ����Ǵ���������С�������꣬�ɵô𰸣�
��4������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��ɵ�MN�ij������ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����ֱ��AC�Ľ���ʽΪy=kx+b����A��C���������룬��
$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$��
ֱ��AC�Ľ���ʽΪy=-x+4��
��2����A��C��������������ߵĽ���ʽ����
$\left\{\begin{array}{l}{-\frac{1}{2}��{4}^{2}+4b+c=0}\\{c=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=1}\\{c=4}\end{array}\right.$��
�����ߵĽ���ʽΪy=-$\frac{1}{2}$x2+x+4��
��3���ߵ�M�ĺ�����Ϊm��
��M���������m��-$\frac{1}{2}$m2+m+4������N��������m��-m+4����
�ٵ���M�ڵ�N���Ϸ�ʱ��MN=-$\frac{1}{2}$2+m+4-��-m+4��=-$\frac{1}{2}$m2+2m��
d=-$\frac{1}{2}$m2+2m��
�ڵ���M�ڵ�N���·�ʱ��MN=-m+4-��-$\frac{1}{2}$m2+m+4��=$\frac{1}{2}$m2-2m��
d=$\frac{1}{2}$m2-2m��
��4��m��ֵΪm1=2��m2=2-2$\sqrt{2}$��m3=2+2$\sqrt{2}$���������£�
�ٵ�M�ڵ�N���Ϸ�ʱ��MN�TOE=2����-$\frac{1}{2}$m2+2m=2��
���m1=m2=2��
��m=2��
�ڵ���M�ڵ�N���·�ʱ��MN=OE=2����$\frac{1}{2}$m2-2m=2��
���m1=2-2$\sqrt{2}$��m2=2+2$\sqrt{2}$��
��m=2-2$\sqrt{2}$��m=2+2$\sqrt{2}$��
�������������Ե�M��N��E��OΪ������ı���Ϊƽ���ı���ʱ��m��ֵΪm1=2��m2=2-2$\sqrt{2}$��m3=2+2$\sqrt{2}$��
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ���������Ľ���ʽ������ƽ����y���ֱ���������ľ����Ǵ���������С���������ǽ���ؼ���Ҫ�������ۣ��Է���©������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��εó�MN�ij��ǽ���ؼ���Ҫ�������ۣ��Է���©��


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
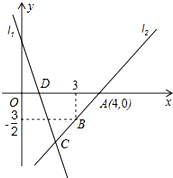 ��ͼ����ֱ֪��l1��y=-3x+3��x�ύ�ڵ�D��ֱ��l2������A��4��0����B��3��-$\frac{3}{2}$��������l1���ڵ�C��
��ͼ����ֱ֪��l1��y=-3x+3��x�ύ�ڵ�D��ֱ��l2������A��4��0����B��3��-$\frac{3}{2}$��������l1���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
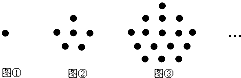 ��ͼͼ�ζ�����ͬ����С�����Ӱ�һ���Ĺ�����ɣ����еڢٸ�ͼ����1�����ӣ��ڢڸ�ͼ��һ����6�����ӣ��ڢ۸�ͼ��һ����16�����ӣ�������ڢ��ͼ�������ӵĿ���Ϊ��������
��ͼͼ�ζ�����ͬ����С�����Ӱ�һ���Ĺ�����ɣ����еڢٸ�ͼ����1�����ӣ��ڢڸ�ͼ��һ����6�����ӣ��ڢ۸�ͼ��һ����16�����ӣ�������ڢ��ͼ�������ӵĿ���Ϊ��������| A�� | 141 | B�� | 106 | C�� | 169 | D�� | 150 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
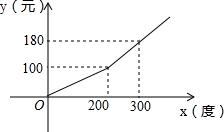 Ϊ���ӹ���Ľ�Լ�õ���ʶ��ij�в��÷ֶμƷѵķ������¼���ÿ����ͥ�ĵ�ѣ�ÿ����ͥÿ�µ��y��Ԫ�����õ���x���ȣ�֮��ĺ���ͼ����ͼ��ʾ��
Ϊ���ӹ���Ľ�Լ�õ���ʶ��ij�в��÷ֶμƷѵķ������¼���ÿ����ͥ�ĵ�ѣ�ÿ����ͥÿ�µ��y��Ԫ�����õ���x���ȣ�֮��ĺ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | 0 | D�� | ������0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ�������������ɸ���ͬ��С�������ɵģ���������ͼ������ͼ��ͬ������ͼ��ʾ�����ü������С��������༸�飿���ټ��飿
һ�������������ɸ���ͬ��С�������ɵģ���������ͼ������ͼ��ͬ������ͼ��ʾ�����ü������С��������༸�飿���ټ��飿�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com