
分析 ①先把各二次根式化为最简二次根式,然后合并即可;
②根据二次根式的除法法则运算;
③利用完全平方公式计算;
④先把各二次根式化为最简二次根式,然后合并即可.
解答 解:①原式=4$\sqrt{3}$+12$\sqrt{3}$-3$\sqrt{3}$
=13$\sqrt{3}$;
②原式=$\sqrt{\frac{50×32}{8}}$-4
=10$\sqrt{2}$-4;
③原式=8-4$\sqrt{6}$+3
=11-4$\sqrt{6}$;
④原式=$\frac{\sqrt{6}}{3}$-24$\sqrt{6}$+7$\sqrt{6}$
=-$\frac{50\sqrt{6}}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
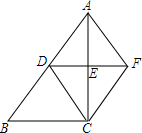 如图,在Rt△ABC中,∠ACB=90°,D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF、CD.
如图,在Rt△ABC中,∠ACB=90°,D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF、CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (7,20) | B. | (20,7) | C. | (7,7) | D. | (20,20) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
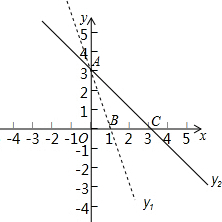 已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).
已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
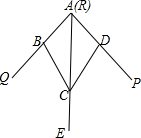 如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2014年12月25日,石家庄至济南客运专线重点控制工程衡景特大桥箱梁架设任务全面展开,该项目在招标时接到了甲、乙两个施工单位的投标书,从投标书中得知如图所示的信息.
2014年12月25日,石家庄至济南客运专线重点控制工程衡景特大桥箱梁架设任务全面展开,该项目在招标时接到了甲、乙两个施工单位的投标书,从投标书中得知如图所示的信息.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com