
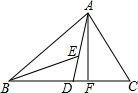
 如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.分析 (1)先利用三角形的外角性质计算出∠ABE=15°,再利用角平分线定义得到∠ABC=2∠ABE=30°,然后根据高的定义和互余可求出∠BAF的度数;
(2)先根据中线定义得到BC=2BD=10,然后利用三角形面积公式求AF的长.
解答 解:(1)∵∠BED=∠ABE+∠BAE,
∴∠ABE=40°-25°=15°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=30°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°-∠ABF=90°-30°=60°;
(2)∵AD为中线,
∴BD=CD=5,
∵S△ABC=$\frac{1}{2}$AF•BC,
∴AF=$\frac{2×40}{10}$=8.
点评 本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质和三角形面积公式.本题的关键是充分应用三角形的角平分线、高和中线的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
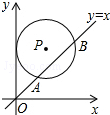 如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.
如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
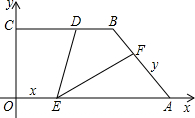 如图,直角梯形OABC的直角顶点O是坐标原点,PA,OC分别在x轴、y轴正半轴上,OA∥BC,D是BC上一点,BD=$\frac{1}{4}OA$=$\sqrt{2}$,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
如图,直角梯形OABC的直角顶点O是坐标原点,PA,OC分别在x轴、y轴正半轴上,OA∥BC,D是BC上一点,BD=$\frac{1}{4}OA$=$\sqrt{2}$,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
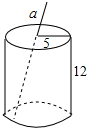 如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )
如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )| A. | 8≤a≤15 | B. | 5≤a≤8 | C. | 7≤a≤8 | D. | 7≤a≤15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
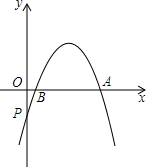 已知二次函数y=ax2+bx+c的图象经过点P(0,$-\frac{5}{2}$)、A(5,0)、B(1,0).
已知二次函数y=ax2+bx+c的图象经过点P(0,$-\frac{5}{2}$)、A(5,0)、B(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com