
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() .反比例函数
.反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
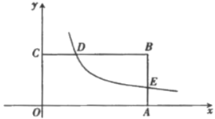
(1)求这个反比例函数的表达式,
(2)动点![]() 在矩形
在矩形![]() 内,且满足
内,且满足![]() .
.
①若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标,
的坐标,
②若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,求点
为顶点的四边形是菱形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①
;(2)① ![]() ;②
;②![]()
【解析】
(1)设点B的坐标为(m,n),则点E的坐标为(m,![]() n),点D的坐标为(m6,n),利用反比例函数图象上点的坐标特征可求出m的值,结合OC:CD=5:3可求出n值,再将m,n的值代入k=
n),点D的坐标为(m6,n),利用反比例函数图象上点的坐标特征可求出m的值,结合OC:CD=5:3可求出n值,再将m,n的值代入k=![]() mn中即可求出反比例函数的表达式;
mn中即可求出反比例函数的表达式;
(2)由三角形的面积公式、矩形的面积公式结合S△PAO=![]() S四边形OABC可求出点P的纵坐标.
S四边形OABC可求出点P的纵坐标.
①若点P在这个反比例函数的图象上,利用反比例函数图象上点的坐标特征可求出点P的坐标;
②由点A,B的坐标及点P的纵坐标可得出AP≠BP,进而可得出AB不能为对角线,设点P的坐标为(t,4),分AP=AB和BP=AB两种情况考虑:(i)当AB=AP时,利用勾股定理可求出t值,进而可得出点P1的坐标,结合P1Q1的长可求出点Q1的坐标;(ii)当BP=AB时,利用勾股定理可求出t值,进而可得出点P2的坐标,结合P2Q2的长可求出点Q2的坐标.综上,此题得解.
解:(1)设点B的坐标为(m,n),则点E的坐标为(m,![]() n),点D的坐标为(m6,n).
n),点D的坐标为(m6,n).
∵点D,E在反比例函数![]() 的图象上,
的图象上,
∴k=![]() mn=(m6)n,
mn=(m6)n,
∴m=9.
∵OC:CD=5:3,
∴n:(m6)=5:3,
∴n=5,
∴k=![]() mn=
mn=![]() ×9×5=15,
×9×5=15,
∴反比例函数的表达式为y=![]() ;
;
(2)∵S△PAO=![]() S四边形OABC,
S四边形OABC,
∴![]() OAyP=
OAyP=![]() OAOC,
OAOC,
∴yP=![]() OC=4.
OC=4.
①当y=4时,![]() =4,
=4,
解得:x=![]() ,
,
∴若点P在这个反比例函数的图象上,点P的坐标为(![]() ,4).
,4).
②由(1)可知:点A的坐标为(9,0),点B的坐标为(9,5),
∵yP=4,yA+yB=5,
∴y P≠![]() ,
,
∴AP≠BP,
∴AB不能为对角线.
设点P的坐标为(t,4).
分AP=AB和BP=AB两种情况考虑(如图所示):
(i)当AB=AP时,(9t)2+(40)2=52,
解得:t1=6,t2=12(舍去),
∴点P1的坐标为(6,4),
又∵P1Q1=AB=5,
∴点Q1的坐标为(6,9);
(ii)当BP=AB时,(9t)2+(51)2=52,
解得:t3=92![]() ,t4=9+2
,t4=9+2![]() (舍去),
(舍去),
∴点P2的坐标为(92![]() ,4).
,4).
又∵P2Q2=AB=5,
∴点Q2的坐标为(92![]() ,1).
,1).
综上所述:点Q的坐标为(6,9)或(92![]() ,1).
,1).



科目:初中数学 来源: 题型:
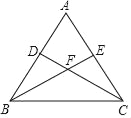
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
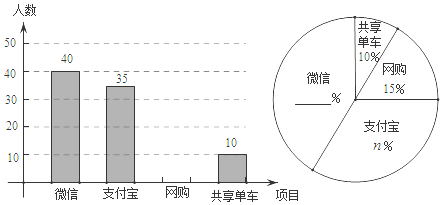
(1)根据图中的信息求出![]() _______,
_______,![]() _______;
_______;
(2)请你帮助他们将这两个统计图补全,并计算扇形统计图中“支付宝”部分所对应的圆心角的度数为_____;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
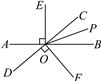
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)图中除直角外,还有其他相等的角,请写出两对:①______________;②______________.
(2)如果∠AOD=40°,那么:
①根据__________,可得∠BOC=________;
②求∠POF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E是正方形ABCD内一点,连接AE,CE.
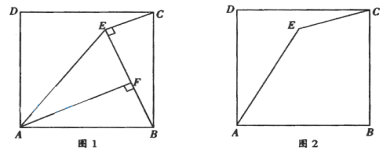
(1)如图1,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.
①证明:![]() ;
;
②求线段![]() 的长.
的长.
(2)如图2,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() ,
,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )
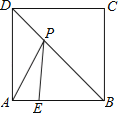
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得![]() ,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
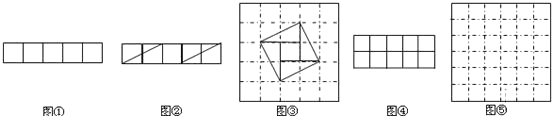
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
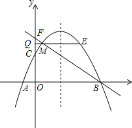
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用勾股定理可以在数轴上画出表示![]() 的点,请依据以下思路完成画图,并保留画图痕迹:
的点,请依据以下思路完成画图,并保留画图痕迹:
第一步:(计算)尝试满足![]() ,使其中a,b都为正整数.你取的正整数a=____,b=________;
,使其中a,b都为正整数.你取的正整数a=____,b=________;
第二步:(画长为![]() 的线段)以第一步中你所取的正整数a,b为两条直角边长画Rt△OEF,使O为原点,点E落在数轴的正半轴上,
的线段)以第一步中你所取的正整数a,b为两条直角边长画Rt△OEF,使O为原点,点E落在数轴的正半轴上, ![]() ,则斜边OF的长即为
,则斜边OF的长即为![]() .
.
请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
第三步:(画表示![]() 的点)在下面的数轴上画出表示
的点)在下面的数轴上画出表示![]() 的点M,并描述第三步的画图步骤:_______________________________________________________________.
的点M,并描述第三步的画图步骤:_______________________________________________________________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com