练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD的边长为4，点E在边AB上，AE＝1，若点P为对角线BD上的一个动点，则△PAE周长的最小值是（　　）

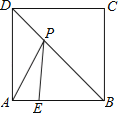
    A.3B.4C.5D.6

    【答案】D

    【解析】

    连接AC、CE，CE交BD于P，此时AP+PE的值最小，求出CE长，即可求出答案．

    解：连接AC、CE，CE交BD于P，连接AP、PE，

    ∵四边形ABCD是正方形，

    ∴OA＝OC，AC⊥BD，即A和C关于BD对称，

    ∴AP＝CP，

    即AP+PE＝CE，此时AP+PE的值最小，

    所以此时△PAE周长的值最小，

    ∵正方形ABCD的边长为4，点E在边AB上，AE＝1，

    ∴∠ABC＝90°，BE＝4﹣1＝3，

    由勾股定理得：CE＝5，

    ∴△PAE的周长的最小值是AP+PE+AE＝CE+AE＝5+1＝6，

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点C在AOB的一边OA上，过点C的直线DE//OB，CF平分ACD，CG CF于C ．

    （1）若O =40，求ECF的度数；

    （2）求证：CG平分OCD；

    （3）当O为多少度时，CD平分OCF，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某批发市场对外批发某品脾的玩具，其价格与件数关系如图所示，请你根据图中描述判断：下列说法中错误的是（ ）

    A. 当件数不超过30件时，每件价格为60元

    B. 当件数在30到60之间时，每件价格随件数增加而减少

    C. 当件数为50件时，每件价格为55元

    D. 当件数不少于60件时，每件价格都是45元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，对角线AC，BD相交于点O，AO＝CO，BO＝DO，且∠ABC+∠ADC＝180°．

    （1）求证：四边形ABCD是矩形；

    （2）若∠ADF：∠FDC＝3：2，DF⊥AC，求∠BDF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．

    （1）求∠CAD的度数；

    （2）延长AC至E，使CE=AC，求证：DA=DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，BD平分∠ABC，且AD⊥BD，E为AC的中点，AD＝6cm，BD＝8cm，BC＝16cm，则DE的长为_____cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，△ABC是等边三角形，P是三角形内一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为18，则PD+PE+PF＝（　　）

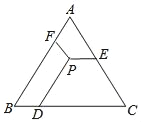
    A. 18B. 9

    C. 6D. 条件不够，不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

    （1）已知：如图1，四边形ABCD的顶点A，B，C在网格格点上，请你在如下的57的网格中画出3个不同形状的等邻边四边形ABCD，要求顶点D在网格格点上；

    （2）如图2，矩形ABCD中，AB=，BC=5，点E在BC边上，连结DE画AFDE于点F，若DE=CD，找出图中的等邻边四边形；

    （3）如图3，在RtABC中，ACB=90°，AB=4，AC=2，D是BC的中点，点M是AB边上一点，当四边形ACDM是“等邻边四边形”时，求BM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，BE与CD相交于点G，且OE=OD，则AP的长为______．

    查看答案和解析>>

    同步练习册答案