
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
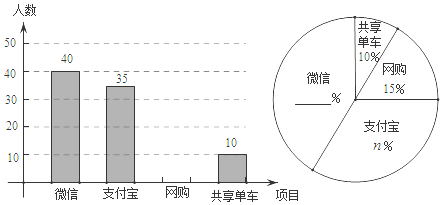
(1)根据图中的信息求出![]() _______,
_______,![]() _______;
_______;
(2)请你帮助他们将这两个统计图补全,并计算扇形统计图中“支付宝”部分所对应的圆心角的度数为_____;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
【答案】(1)![]() 100,
100,![]() 35;(2)126°;(3)大约有800人最认可“微信”这一新生事物.
35;(2)126°;(3)大约有800人最认可“微信”这一新生事物.
【解析】
(1)利用选择共享单车的人数和所占百分比可求出m的值,进而可求出选择支付宝的人数所占百分比,即可得n的值;
(2)用总人数m乘以网购所占百分比即可求出选择网购的人数,可补全条形统计图,根据共享单车、网购、支付宝所占百分比即可求出微信所占百分比,补全扇形统计图即可;根据支付宝所占百分比乘以360°即可求出对应的圆心角的度数;
(3)用2000乘以微信所占百分比即可得答案.
(1)m=10÷10%=100,
35÷100=35%,即n=35,
故答案为:100,35
(2)选择网购的人数为:100×15%=15(人),
微信所占百分比为:1-10%-15%-35%=40%,
∴补全两个统计图如下:
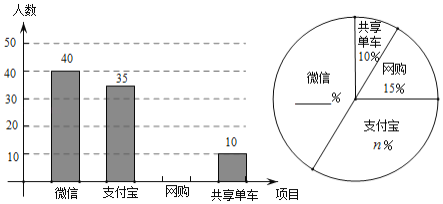
“支付宝”部分所对应的圆心角的度数为360°×35%=126°;
故答案为:126°
(3)2000×40%=800(人).
答:大约有800人最认可“微信”这一新生事物.


科目:初中数学 来源: 题型:
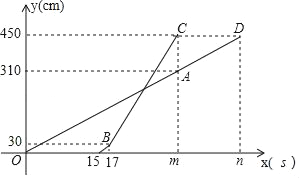
【题目】甲、乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,并且匀速走完全程,乙出发一段时间后速度提高为原来的2倍.设甲行走的时间为x(s),甲、乙行走的路程分别为y1(cm)、y2(cm),y1、y2与x之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙比甲晚出发 s,乙提速前的速度是每秒 cm,m= ,n= ;
(2)当x为何值时,乙追上了甲?
(3)在乙提速后到甲、乙都停止的这段时间内,当甲、乙之间的距离不超过20cm时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
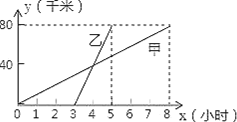
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)甲先出发______小时后,乙才出发;大约在甲出发______小时后,两人相遇,这时他们离A地_______千米.
(2)两人的行驶速度分别是多少?
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
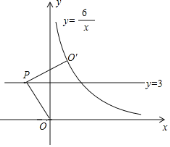
【题目】如图,点P是直线y=3上的动点,连接PO并将PO绕P点旋转90°到PO′,当点O′刚好落在双曲线![]() (x>0)上时,点P的横坐标所有可能值为_____.
(x>0)上时,点P的横坐标所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.
(1)求购买一个甲奖品和一个乙奖品各需多少元?
(2)经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() .反比例函数
.反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
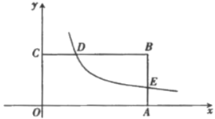
(1)求这个反比例函数的表达式,
(2)动点![]() 在矩形
在矩形![]() 内,且满足
内,且满足![]() .
.
①若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标,
的坐标,
②若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,求点
为顶点的四边形是菱形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=![]() ∠BAC,其中正确的结论有_____________。
∠BAC,其中正确的结论有_____________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com