Question

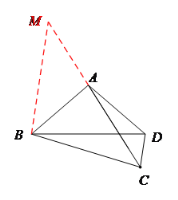
【题目】如图，四边形ABCD中，AB＝AD，BC＝BD，若∠ABD＝∠BAC＝，则∠BDC的度数为( )

A. 2B. 45°＋C. 90°－D. 180°－3

Answer 1

【答案】A

【解析】

作∠MBA＝∠DBA,交CA延长线于M．由∠ABD＝∠ADB＝,∠BAC＝2,得∠CAD＝180°－4,易证△BAM≌△BAD,得∠M＝∠ADB＝,BM＝BD＝BC,设∠ACD＝x，则∠BDC＝x＋，故x＋(x＋)＝＋＋,解得x＝，故∠BDC＝2

作∠MBA＝∠DBA,交CA延长线于M．∠ABD＝∠ADB＝,∠BAC＝2,

∴∠CAD＝180°－4,

∴∠BAM＝180°－2,∠BAD＝180°－2,

∴△BAM≌△BAD,

∴∠M＝∠ADB＝,BM＝BD＝BC,

∴AB＝AM,

∴∠ABM＝∠M＝,

∴∠ACB＝∠M＝,

设∠ACD＝x，则∠BDC＝x＋，

由八字形得x＋(x＋)＝＋＋,

∴x＝，

∴∠BDC＝2