
����Ŀ�����ڡ��¹ڷ��ס��ķ������г��Ϸ������ֳ���������ijҩ���һ����2000Ԫ�������ɸ��������֣���������2.5Ԫ/�����ۣ��ܿ��������ڸ÷������ֳ������ڶ��ι���ʱ��ÿ���������ֵĽ��۱ȵ�һ�εĽ��������25%����ҩ����3000Ԫ�����������ֵ������ȵ�һ�ζ���200�������Ѷ������20%�������ۣ�
��1����һ�ι���ʱ��ÿ���������ֵļ۸��Ƕ���Ԫ��
��2���ڶ����۳�800����������ʱ����������������ҩ����㽵������ʣ��ķ������֣���ô��ҩ��ÿ�������������ཱུ�۶���Ԫ���ۣ�����ʹ�ڶ������۵ķ������ֲ�������
���𰸡���1����һ�ι���ʱ��ÿ���������ֵļ۸���2Ԫ����2����ҩ��ÿ�������������ཱུ��1.5Ԫ���ۣ�����ʹ�ڶ������۵ķ������ֲ�������
��������
��1�����һ�ι���ʱ��ÿ���������ֵļ۸���xԪ����ڶ��ι���ʱ��ÿ���������ֵļ۸��ǣ�1+25%��xԪ�������������ܼۡµ��۽�ϵڶ��αȵ�һ�ζ��200�������ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2���������ν������ۼ�Ĺ�ϵ������ڶ��ι����������ֵĵ��ۣ�����������ܼۡµ��ۼ����۱�ԭ�۸�20%��������ڶ��ι����������ֵ����������۵��ۣ����ҩ��ÿ���������ֽ���yԪ���ۣ����������ܼۣ����۵��ۡ�������ϵڶ������۵ķ������ֲ����������ɵó�����y��һԪһ�β���ʽ����֮ȡ���е����ֵ���ɵó����ۣ�
�⣺��1�����һ�ι���ʱ��ÿ���������ֵļ۸���xԪ����ڶ��ι���ʱ��ÿ���������ֵļ۸��ǣ�1+25%��xԪ��
�����⣬�ã�![]() ��
��![]() ��200��
��200��
��ã�x��2��
�����飬x��2��ԭ��ʽ���̵Ľ⣬�ҷ������⣮
�𣺵�һ�ι���ʱ��ÿ���������ֵļ۸���2Ԫ��
��2���ڶ��ι����������ֵĵ���Ϊ��1+25%����2��2.5��Ԫ����
�ڶ��ι����������ֵ�����Ϊ3000��2.5��1200��������
�ڶ��ι����������ֵ����۵���Ϊ2.5����1+20%����3��Ԫ����
���ҩ��ÿ���������ֽ���yԪ���ۣ�
�����⣬�ã�800��3+��1200��800����3��y����3000��
��ã�y��1.5��
�𣺸�ҩ��ÿ�������������ཱུ��1.5Ԫ���ۣ�����ʹ�ڶ������۵ķ������ֲ�������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
2+22=23��2��
2+22+23=24��2��
2+22+23+24=25��2��
2+22+23+24+25=26��2��
��
��֪��һ���������е�һ������220��221��222��223��224������238��239��240����220=m����220+221+222+223+224+��+238+239+240=_____(����ú�m�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¹������ܵĹ��£����ô�ͬһ�ص�ͬʱ���������Ӻܿ���ڹ�ԶԶ˦�ں�ͷ���������������Ӿ����Լ�ңң���ȣ�������·�ߺ�����˯����������һ�������������ڹ��Ѿ������������Ƿ���ֱ�����ͬʱ�����յ㣮��S1��S2�ֱ��ʾ�ڹ���������ܵ�·�̣�tΪ����ʱ�䣬������ͼ���������������Ǻϵ��ǣ�������
A.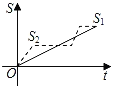 B.
B.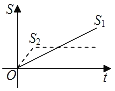
C.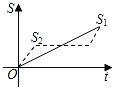 D.
D.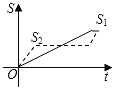
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
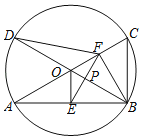
����Ŀ����ͼ����֪AC��BDΪ��O������ֱ��������AB��BC��OE��AB�ڵ�E����F�ǰ뾶OC���е㣬����EF��
��1������O�İ뾶Ϊ1������BAC��30�������߶�EF�ij���
��2������BF��DF����OB��EF���ڵ�P��
����֤��PE��PF��
����DF��EF������BAC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
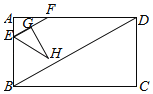
����Ŀ����ͼ������ABCD�У�AB��6����ABD��60������E�ӵ�A��������ÿ��2����λ���ȵ��ٶ��ر�AB�˶�������Bֹͣ�˶�������E��EF��BD��AD�ڵ�F������AEF�Ƶ�E˳ʱ����ת�õ���GEH���ҵ�G�����߶�EF�ϣ����E���˶�ʱ��Ϊt���룩��0��t��3����
��1����t��1������GEH�������
��2������G�ڡ�ABD��ƽ�����ϣ���BE�ij���
��3������GEH����ABD�ص����ֵ����ΪT���ú�t��ʽ�ӱ�ʾT����ֱ��д����0��t��3ʱT��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
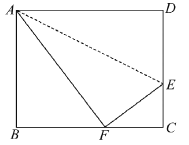
����Ŀ����ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪�ۺ�AE��5![]() cm�� ��tan��EFC��
cm�� ��tan��EFC��![]() ����ô����ABCD���ܳ�_____________cm��
����ô����ABCD���ܳ�_____________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
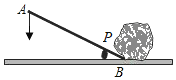
����Ŀ���øܸ���ʯͷ��ʾ��ͼ��ͼ��ʾ��P��֧�㣬������ѹ�ܸ˵�A��ʱ���ܸ���P��ת������һ��B��������ʯͷ�ͱ��˶�������һ��ʯͷҪʹ��������ܸ˵�B�˱�����������8cm����֪�ܸ˵Ķ�����AP��������BP֮��Ϊ4��1��Ҫʹ���ʯͷ����������Ҫ���ܸ˵�A������ѹ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ���Ƴ��������շѷ�ʽ��
��ʽһ���˿��ȹ����Ա����ÿ�Ż�Ա��200Ԫ�����ޱ���һ����ʹ�ã�ƾ����Ӿ��ÿ����Ӿ�ٸ���30Ԫ��
��ʽ�����˿Ͳ������Ա����ÿ����Ӿ����40Ԫ��
��С����һ����������Ӿ����Ӿ�Ĵ���Ϊ![]() �Σ�
��![]() ����������
����������
��1���������⣬��д�±���
��Ӿ���� | 5 | 10 | 15 | �� |
|
��ʽһ���ܷ��ã�Ԫ�� | 350 | 650 | �� | ||
��ʽ�����ܷ��ã�Ԫ�� | 200 | 400 | �� |
��2����С���ƻ�������Ӿ���ܷ���Ϊ2000Ԫ��ѡ�����ָ��ѷ�ʽ������Ӿ�Ĵ����Ƚ϶ࣻ
��3����![]() ʱ��С��ѡ�����ָ��ѷ�ʽ�����㣮��˵������.
ʱ��С��ѡ�����ָ��ѷ�ʽ�����㣮��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ������
������![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.
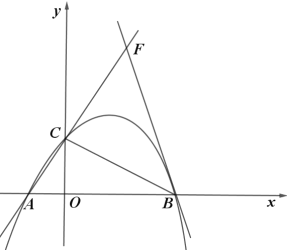
��1���������ߵĺ�������ʽ��
��2����![]() Ϊ
Ϊ![]() ���Ҳ���������һ�㣬�Ƿ���ڵ�
���Ҳ���������һ�㣬�Ƿ���ڵ�![]() ʹ
ʹ![]() �������ڣ������
�������ڣ������![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
��3����ֱ��![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����ֱ��
����ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ֱ��
����ֱ��![]() �ĺ�������ʽ.
�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com