
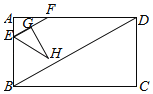
【题目】如图,矩形ABCD中,AB=6,∠ABD=60°,点E从点A出发,以每秒2个单位长度的速度沿边AB运动,到点B停止运动.过点E作EF∥BD交AD于点F,将△AEF绕点E顺时针旋转得到△GEH,且点G落在线段EF上,设点E的运动时间为t(秒)(0<t<3).
(1)若t=1,求△GEH的面积;
(2)若点G在∠ABD的平分线上,求BE的长;
(3)设△GEH与△ABD重叠部分的面积为T,用含t的式子表示T,并直接写出当0<t<3时T的取值范围.
【答案】(1)2![]() ;(2)3;(3)T=
;(2)3;(3)T=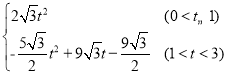 .
.
【解析】
(1)根据四边形ABCD是矩形和EF∥BD,可推出AE和AF的长,即可求出答案;
(2)由BG平分∠ABD,可得∠EBG=![]() ∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
(3)当点H落在BD上时,作EJ⊥BD于J,根据EF∥BD,推出△EBH是等边三角形,从而得出t=1,再分当0<t≤1时和当1<t<3时两种情况讨论即可.
解:(1)如图1中,
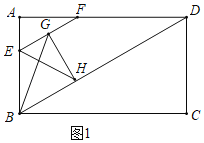
∵四边形ABCD是矩形,
∴∠A=90°,
∵EF∥BD,
∴∠AEF=60°,
∵AE=2,
∴AF=AEtan60°=![]() ,
,
∴S△EGH=S△AEF=![]() AEAF=
AEAF=![]() ×2×
×2×![]() =
=![]() ;
;
(2)如图2中,
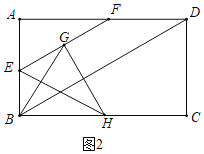
由题意得,BG平分∠ABD,
∴∠EBG=![]() ∠ABD=30°,
∠ABD=30°,
∵∠AEG=∠EBG+∠EGB=60°,
∴∠EBG=∠EGB=30°,
∴BE=EG=AE=3;
(3)如图1﹣1中,当点H落在BD上时,作EJ⊥BD于J,
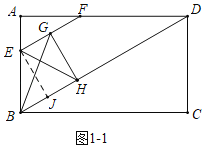
∵EF∥BD,
∴∠FEH=∠EHB=60°,
∴△EBH是等边三角形,
∴EH=EB=EF=2AE,
∴AE=2,BE=4,
∴t=1,
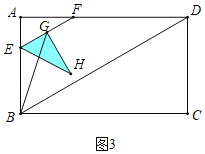
如图3中,当0<t≤1时,重叠部分是△EGH,T=S△AEF=![]() ×2t×2t×
×2t×2t×![]() =
=![]() t2,
t2,
如图4中,当1<t<3时,重叠部分是四边形MNGE,作EJ⊥BD于J,
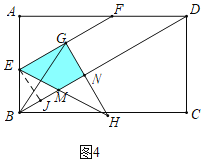
在Rt△EBJ中,∵BE=6﹣2t,∠EBJ=60°,
∴BJ=![]() BE=3﹣t,EJ=
BE=3﹣t,EJ=![]() BJ=3
BJ=3![]() ﹣
﹣![]() t,
t,
∵△EBM是等边三角形,
∴BJ=JM=3﹣t,
∵四边形EGNJ是矩形,
∴EG=NJ=2t,
∴MN=NJ﹣MJ=3t﹣3,
∴T=![]() (MN+EG)EJ=
(MN+EG)EJ=![]() (3t﹣3+2t)(3
(3t﹣3+2t)(3![]() ﹣
﹣![]() t)=
t)=![]() t2+9
t2+9![]() t
t![]() ,
,
综上所述,T=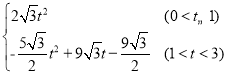 .
.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
(1)求AB的长;
(2)求证:四边形ACED是菱形;
(3)设点C的坐标为(0,![]() ),△ECD与△AOB重合部分的面积为
),△ECD与△AOB重合部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
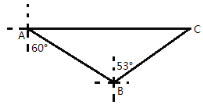
【题目】知识改变世界,科技改变生活。导航设备的不断更新方便了人们的出行。如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位)
(参考数据![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
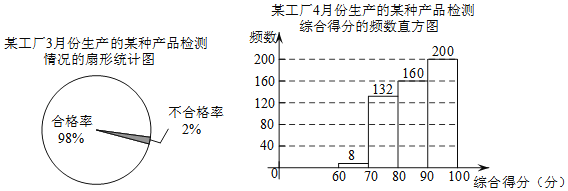
【题目】某工厂生产某种产品,3月份的产量为5000件,4月份的产量为10000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.
(1)求4月份生产的该产品抽样检测的合格率;
(2)在3月份和4月份生产的产品中,估计哪个月的不合格件数最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
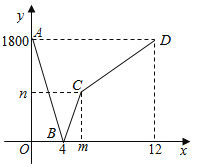
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“新冠肺炎”的发生,市场上防护口罩出现热销.某药店第一次用2000元购进若干个防护口罩,并按定价2.5元/个出售,很快售完由于该防护口罩畅销,第二次购进时,每个防护口罩的进价比第一次的进价提高了25%,该药店用3000元购进防护口罩的数量比第一次多了200个,并把定价提高20%进行销售.
(1)第一次购进时,每个防护口罩的价格是多少元?
(2)第二次售出800个防护口罩时,出现了滞销,该药店打算降价售完剩余的防护口罩.那么该药店每个防护口罩至多降价多少元出售,才能使第二次销售的防护口罩不亏本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
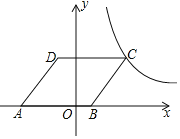
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
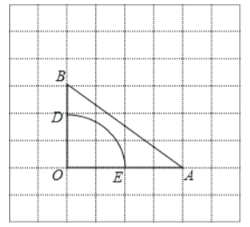
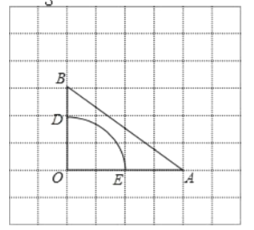
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均在格点上,
均在格点上,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
(1)![]() 的长为 ;
的长为 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() (
(![]() ) ,连接
) ,连接![]() .
.
①如图 1,若![]() 是
是![]() 的中点,请在网格中画出
的中点,请在网格中画出![]() ,使
,使![]() ;
;
②如图 2,连接![]() ,请在网格中画出点
,请在网格中画出点![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com