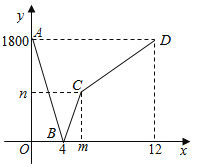
【题目】甲、乙两地高速铁路建设成功，一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车均匀速行驶并同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示y与x之间的函数关系，下列说法：
①甲、乙两地相距1800千米；
②点B的实际意义是两车出发后4小时相遇；
③m＝6，n＝900；
④动车的速度是450千米/小时．
其中不正确的是（ ）
A.①B.②C.③D.④
科目：初中数学 来源： 题型：
【题目】某企业承接了27000件产品的生产任务，计划安排甲、乙两个车间的共50名工人，合作生产20天完成．已知甲、乙两个车间利用现有设备，工人的工作效率为：甲车间每人每天生产25件，乙车间每人每天生产30件．
（1）求甲、乙两个车间各有多少名工人参与生产?
（2）为了提前完成生产任务，该企业设计了两种方案：
方案一 甲车间租用先进生产设备，工人的工作效率可提高20%，乙车间维持不变．
方案二 乙车间再临时招聘若干名工人（工作效率与原工人相同），甲车间维持不变．
设计的这两种方案，企业完成生产任务的时间相同．
①求乙车间需临时招聘的工人数；
②若甲车间租用设备的租金每天900元，租用期间另需一次性支付运输等费用1500元；乙车间需支付临时招聘的工人每人每天200元．问：从新增加的费用考虑，应选择哪种方案能更节省开支？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xoy中，直线
（k为常数）与抛物线
交于A,B两点，且A点在
轴右侧，P点的坐标为（0,4）连接PA,PB.(1)△PAB的面积的最小值为____；（2）当
时，
=_______
查看答案和解析>>
科目：初中数学 来源： 题型：
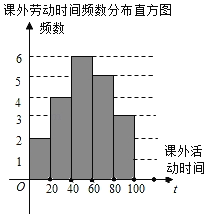
【题目】遵义市各校都在深入开展劳动教育，某校为了解七年级学生一学期参加课外劳动时间（单位：h）的情况，从该校七年级随机抽查了部分学生进行问卷调查，并将调查结果绘制成如下不完整的频数分布表和频数分布直方图．
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t＜20 | 2 | 0.1 |
20≤t＜40 | 4 | m |
40≤t＜60 | 6 | 0.3 |
60≤t＜80 | a | 0.25 |
80≤t＜100 | 3 | 0.15 |
解答下列问题：
（1）频数分布表中a＝ ，m＝ ；将频数分布直方图补充完整；
（2）若七年级共有学生400人，试估计该校七年级学生一学期课外劳动时间不少于60h的人数；
（3）已知课外劳动时间在60h≤t＜80h的男生人数为2人，其余为女生，现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛，请用树状图或列表法求所选学生为1男1女的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设函数y1＝
，y2＝﹣（k＞0）．
（1）当2≤x≤3时，函数y1的最大值是a，函数y2的最小值是a﹣4，求a和k的值．
（2）设m≠0，且m≠﹣1，当x＝m时，y1＝p；当x＝m+1时，y1＝q．圆圆说：“p一定大于q”．你认为圆圆的说法正确吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
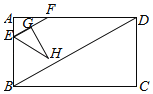
【题目】如图，矩形ABCD中，AB＝6，∠ABD＝60°，点E从点A出发，以每秒2个单位长度的速度沿边AB运动，到点B停止运动．过点E作EF∥BD交AD于点F，将△AEF绕点E顺时针旋转得到△GEH，且点G落在线段EF上，设点E的运动时间为t（秒）（0＜t＜3）．
（1）若t＝1，求△GEH的面积；
（2）若点G在∠ABD的平分线上，求BE的长；
（3）设△GEH与△ABD重叠部分的面积为T，用含t的式子表示T，并直接写出当0＜t＜3时T的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
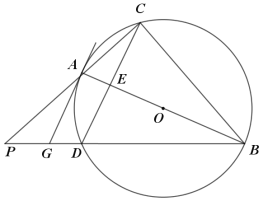
【题目】如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，将△ABC沿直线AB折叠得到△ABD，交⊙O于点D．连接CD交AB于点E，延长BD和CA相交于点P，过点A作AG∥CD交BP于点G．
（1）求证：直线GA是⊙O的切线；
（2）求证：AC2＝GDBD；
（3）若tan∠AGB＝
，PG＝6，求cos∠P的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
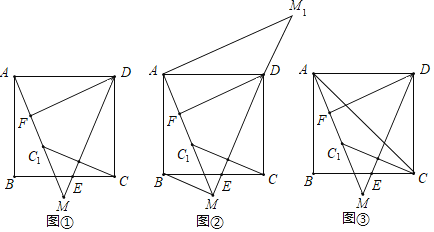
【题目】如图，在正方形ABCD中，点E是边BC上任意一点（点E不与点B、C重合），连结DE，点C关于DE的对称点为C1，连结AC1并延长交DE的延长线于点M，F是AC1的中点，连结DF．
（猜想）如图①，∠FDM的大小为 度．
（探究）如图②，过点A作AM1∥DF交MD的延长线于点M1，连结BM．求证：△ABM≌△ADM1．
（拓展）如图③，连结AC，若正方形ABCD的边长为2，则△ACC1面积的最大值为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
