
【题目】设![]() 都是整数,且每个数都满足
都是整数,且每个数都满足![]() 都满足
都满足![]() ,若
,若![]()
![]() 的最小值是
的最小值是![]() 的最小值是
的最小值是![]() ,...,则
,...,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据已知得出a15+a25+…+a20125=-a+b+32d=100+30d,再利用取最小值与最大值得出d与b的值,进而分析得出答案.
解:因为-1≤ai≤2.
所以设有a个-1,b个1,c个0,d个2,
因为a1+a2+……+a2020=100,
所以-a+b+2d=100,
所以-a+b+8d=100+6d,-a+b+32d=100+30d,
因为a13+a23+…+a20203的最小值是106,a15+a25+…+a20205的最小值是130,
所以d=1,
……,
所以-a+b+512d=100+510d=610,
所以a19+a29+……+a20209的最小值是610.
故选:D.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
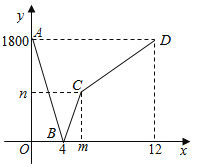
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
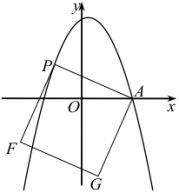
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),直线l的解析式为y=-x+b,且与x轴,y轴分别交于点A、B.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,与x轴,y轴分别交于点C,D,运动时间为t秒(0≤t≤b),将△OCD沿着直线m翻折得到△ECD.若△ECD和△OAB的重合部分的面积为S(设t=0或b时,S=0),且S与t之间的函数关系的图象如图(2)所示,则图象中的最高点P的坐标是( )
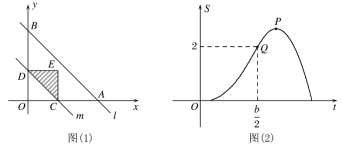
A.(![]() ,3)B.(3,3)C.(
,3)B.(3,3)C.(![]() ,
,![]() )D.(3,
)D.(3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家“垃圾分类进校园”的号召,某校准备购买新的分类垃圾箱进行更换,已知购买5个A类垃圾箱和4个B类垃圾箱需花费1600元,购买3个A类垃圾箱的费用恰好等于购买4个B类垃圾箱的费用.
(1)求购买一个A类垃圾箱和一个B类垃圾箱各需多少元;
(2)该校计划用不超过9000元的经费购买A类和B类垃圾箱共50个,其中A类垃圾箱的数量不低于25个,则本次可以选择的方案有几种;
(3)在(2)的条件下哪种方案的费用最低,最低费用是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
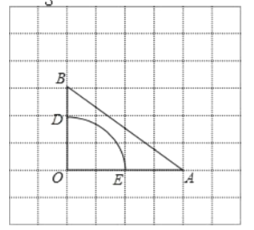
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均在格点上,
均在格点上,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
(1)![]() 的长为 ;
的长为 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() (
(![]() ) ,连接
) ,连接![]() .
.
①如图 1,若![]() 是
是![]() 的中点,请在网格中画出
的中点,请在网格中画出![]() ,使
,使![]() ;
;
②如图 2,连接![]() ,请在网格中画出点
,请在网格中画出点![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
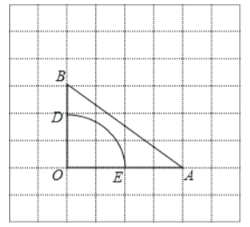
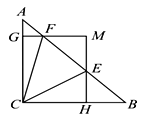
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②AF+BE=EF;③当点E与点B重合时,MH=
;②AF+BE=EF;③当点E与点B重合时,MH=![]() ;其中正确结论的个数是( )
;其中正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“购买![]() 张彩票就中奖”是不可能事件
张彩票就中奖”是不可能事件
B.“概率为![]() 的事件”是不可能事件
的事件”是不可能事件
C.“任意画一个六边形,它的内角和等于![]() ”是必然事件
”是必然事件
D.从![]() 中任取
中任取![]() 个不同的数,分别记为
个不同的数,分别记为![]() 和
和![]() ,那么
,那么![]() 的概率是
的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com