
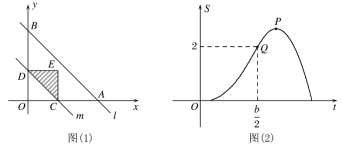
【题目】如图(1),直线l的解析式为y=-x+b,且与x轴,y轴分别交于点A、B.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,与x轴,y轴分别交于点C,D,运动时间为t秒(0≤t≤b),将△OCD沿着直线m翻折得到△ECD.若△ECD和△OAB的重合部分的面积为S(设t=0或b时,S=0),且S与t之间的函数关系的图象如图(2)所示,则图象中的最高点P的坐标是( )
A.(![]() ,3)B.(3,3)C.(
,3)B.(3,3)C.(![]() ,
,![]() )D.(3,
)D.(3,![]() )
)
【答案】C
【解析】
先根据(![]() ,2)求出直线的解析式,再根据解析式求出A、B的坐标,计算
,2)求出直线的解析式,再根据解析式求出A、B的坐标,计算![]() 的面积,然后用t表示出重合部分的面积,根据题意列出方程即可得到答案.
的面积,然后用t表示出重合部分的面积,根据题意列出方程即可得到答案.
在题干图1位置,S△MNP=![]() t2,将(
t2,将(![]() ,2)代入S△MNP=
,2)代入S△MNP=![]() t2,得:
t2,得: ![]() ,解得
,解得![]() (负值舍去),
(负值舍去),
即直线l的解析式为y=-x+4.
所以,A(4,0),B(0,4).
所以,S△ABO=![]() OA·OB=
OA·OB=![]() ×4×4=8,
×4×4=8,
如图,当0<t≤2时,S△MNP=![]() t2,
t2,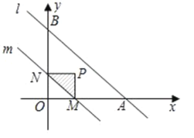
当t=2时,S△MNP最大,S△MNP=![]() t2=
t2=![]() ×22=2,
×22=2,
如图,当2<t≤4时,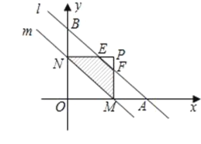
S1=S△ABO-S△OMN-2S△MAF,
即S1=![]()
=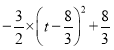
当![]() 时,S1最大=
时,S1最大=![]() ,
,
因为S1>S△MNP,
所以此时为面积的最大值,则最高点P的坐标(![]() ,
,![]() )
)
故选:C


科目:初中数学 来源: 题型:
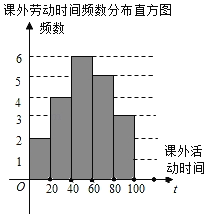
【题目】遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列问题:
(1)频数分布表中a= ,m= ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;
(3)已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
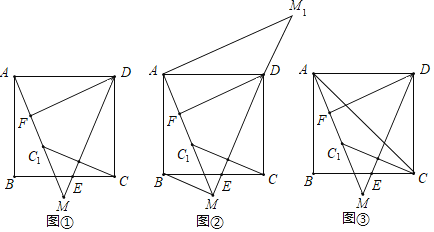
【题目】如图,在正方形ABCD中,点E是边BC上任意一点(点E不与点B、C重合),连结DE,点C关于DE的对称点为C1,连结AC1并延长交DE的延长线于点M,F是AC1的中点,连结DF.
(猜想)如图①,∠FDM的大小为 度.
(探究)如图②,过点A作AM1∥DF交MD的延长线于点M1,连结BM.求证:△ABM≌△ADM1.
(拓展)如图③,连结AC,若正方形ABCD的边长为2,则△ACC1面积的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() (顶点是网格线的交点)和直线l及点O.
(顶点是网格线的交点)和直线l及点O.
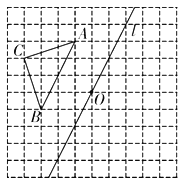
(1)画出![]() 关于直线l对称的
关于直线l对称的![]() ;
;
(2)连接OA,将OA绕点O顺时针旋转![]() ,画出旋转后的线段;
,画出旋转后的线段;
(3)在旋转过程中,当OA与![]() 有交点时,旋转角
有交点时,旋转角![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全球关注的抗击“新冠肺炎”中某跨国科研中心的一个团队研制了一种助治“新冠附炎”的新药,在试验药效时发现,如果成人按规定的制量服用,那么服药后2小时血液中含药量最高,达每毫升8微克(1微克=![]() 毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量
毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示.
(小时)的变化如图所示.
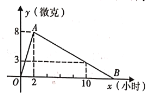
(1)分别求线段![]() 所表示的函数关系式;
所表示的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时对治病是有效的,那么这个有效时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点D是AB下方圆上的一点,点C是优弧AD的中点,过点B作⊙O的切线BE交AC的延长线于点E,连接OC,OD,CB,BD.
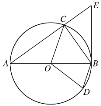
(1)求证:BD∥OC;
(2)当AB=6时,完成填空:
①当BE= 时,四边形ODBC是菱形;
②当BE= 时,S△BCE=![]() S△ABC.
S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
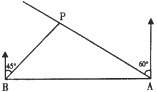
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
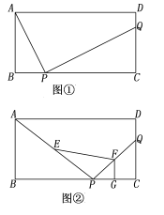
【题目】已知:如图①,②,在矩形ABCD中,AB=4,BC=8,P,Q分别是边BC,CD上的点.
(1)如图①,若AP⊥PQ,BP=2,求CQ的长;
(2)如图②,若![]() =2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
=2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com