
【题目】如图,AB为⊙O的直径,点D是AB下方圆上的一点,点C是优弧AD的中点,过点B作⊙O的切线BE交AC的延长线于点E,连接OC,OD,CB,BD.
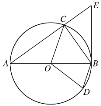
(1)求证:BD∥OC;
(2)当AB=6时,完成填空:
①当BE= 时,四边形ODBC是菱形;
②当BE= 时,S△BCE=![]() S△ABC.
S△ABC.
【答案】(1)见解析;(2)①![]() ; ②3
; ②3
【解析】
(1)连接CD,根据圆的基本性质可得AC=DC,然后证出![]() ≌
≌![]() ,可得∠A=∠ODC,然后根据同弧所对的圆周角性质可得∠A=∠CDB,再推出∠OCD=∠CDB即可证出结论;
,可得∠A=∠ODC,然后根据同弧所对的圆周角性质可得∠A=∠CDB,再推出∠OCD=∠CDB即可证出结论;
(2)①根据切线的性质可得∠ABE=90°,当AB=6,BE=![]() 时,利用锐角三角函数即可求出∠A,从而求出∠COB和∠ODB,根据等边三角形的判定定理可证
时,利用锐角三角函数即可求出∠A,从而求出∠COB和∠ODB,根据等边三角形的判定定理可证![]() 和
和![]() 都是等边三角形,从而得出BC=OC=OD=BD,即可证出结论;
都是等边三角形,从而得出BC=OC=OD=BD,即可证出结论;
②根据切线的性质可得∠ABE=90°,当AB=6,BE=3时,利用锐角三角函数即可求出tanA,从而得出![]() ,设BC=x,利用勾股定理求出BC和AC,再利用勾股定理即可求出CE,即可求出CE:AC,然后根据两个三角形等高时,面积比等于底之比即可得出结论.
,设BC=x,利用勾股定理求出BC和AC,再利用勾股定理即可求出CE,即可求出CE:AC,然后根据两个三角形等高时,面积比等于底之比即可得出结论.
(1)证明:连接CD,
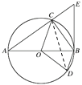
∵点C为优弧AD的中点,
∴AC=DC.
又∵OA=OD,OC=OC,
∴![]() ≌
≌![]() ,
,
∴∠A=∠ODC.
又∵∠A与∠CDB都为![]() 所对的圆周角,
所对的圆周角,
∴∠A=∠CDB,
∴∠ODC=∠CDB.
∵OD=OC,
∴∠ODC=∠OCD,
∴∠OCD=∠CDB
∴BD∥OC.
(2)解:①当BE=![]() 时,四边形ODBC是菱形,理由如下
时,四边形ODBC是菱形,理由如下
∵BE为⊙O的切线
∴∠ABE=90°
当AB=6,BE=![]() 时,
时,
∴tanA=![]()
∴∠A=30°
∴∠COB=2∠A=60°,∠ODB=∠ODC+∠CDB=2∠A=60°
∵OC =OB=OD
∴![]() 和
和![]() 都是等边三角形
都是等边三角形
∴BC=OC=OD=BD
∴四边形ODBC是菱形
故答案为:![]() ;
;
②当BE=3时,S△BCE=![]() S△ABC,理由如下
S△ABC,理由如下
∵BE为⊙O的切线
∴∠ABE=90°
当AB=6,BE=3时,
∴tanA=![]()
∵AB为直径
∴∠ACB=90°
∴tanA=![]()
设BC=x,则AC=2x
∴BC2+AC2=AB2
即x2+(2x)2=62
解得:x=![]() 或
或![]() (不符合实际,舍去)
(不符合实际,舍去)
∴BC=![]() ,AC=
,AC=![]()
在Rt△BCE中,CE=![]()
∴CE:AC=![]() :
:![]() =1:4
=1:4
∴S△BCE:S△ABC=1:4
∴S△BCE=![]() S△ABC.
S△ABC.
故答案为:3 .


科目:初中数学 来源: 题型:
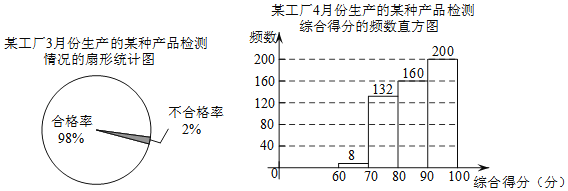
【题目】某工厂生产某种产品,3月份的产量为5000件,4月份的产量为10000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.
(1)求4月份生产的该产品抽样检测的合格率;
(2)在3月份和4月份生产的产品中,估计哪个月的不合格件数最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
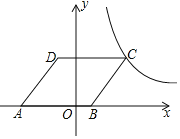
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),直线l的解析式为y=-x+b,且与x轴,y轴分别交于点A、B.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,与x轴,y轴分别交于点C,D,运动时间为t秒(0≤t≤b),将△OCD沿着直线m翻折得到△ECD.若△ECD和△OAB的重合部分的面积为S(设t=0或b时,S=0),且S与t之间的函数关系的图象如图(2)所示,则图象中的最高点P的坐标是( )
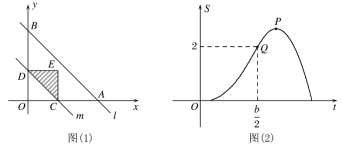
A.(![]() ,3)B.(3,3)C.(
,3)B.(3,3)C.(![]() ,
,![]() )D.(3,
)D.(3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均在格点上,
均在格点上,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).
(1)![]() 的长为 ;
的长为 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() (
(![]() ) ,连接
) ,连接![]() .
.
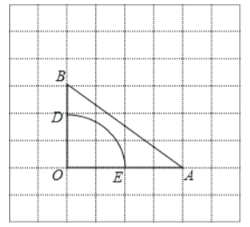
①如图 1,若![]() 是
是![]() 的中点,请在网格中画出
的中点,请在网格中画出![]() ,使
,使![]() ;
;
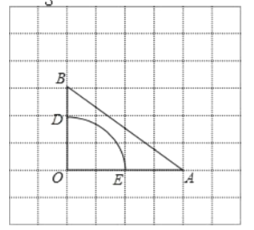
②如图 2,连接![]() ,请在网格中画出点
,请在网格中画出点![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
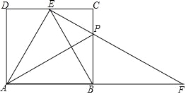
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
①点B平分线段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正确结论的序号是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的对角线AC,BD交于点O,DE平分∠ADC交BC于点E,交AC与点F,且∠BCD=60°,BC=2CD,连接OE,则下列结论:①OE∥AB ②SABCD=BD·CD ③AO=2BO ④S△DOF=2S△EOF,其中成立的有( )
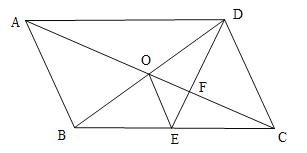
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com