
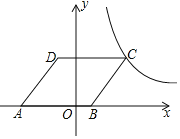
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.
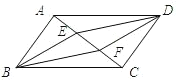
(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
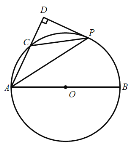
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE按如图所示方式放置,点D在△ABC内,连接BD、CD和CE,且∠DCE=90°.

(1)如图①,当△ABC和△ADE均为等边三角形时,试确定AD、BD、CD三条线段的关系,并说明理由;
(2)如图②,当BA=BC=2AC,DA=DE=2AE时,试确定AD、BD、CD三条线段的关系,并说明理由;
(3)如图③,当AB:BC:AC=AD:DE:AE=m:n:p时,请直接写出AD、BD、CD三条线段的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
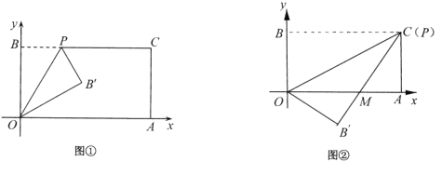
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
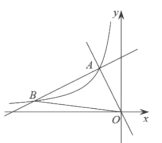
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中数学 来源: 题型:
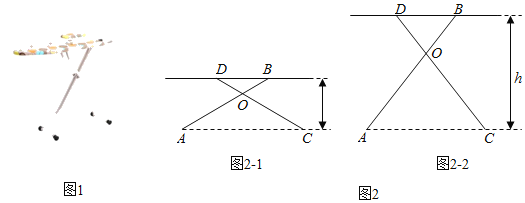
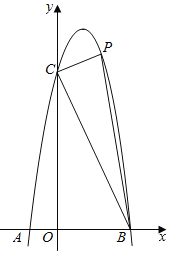
【题目】如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
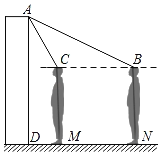
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com