
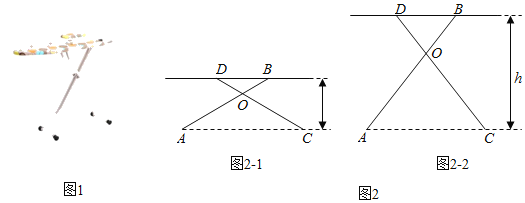
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,为加快5G网络建设,某通信公司在一个坡度i=1:2.4的山坡AB上建了一座信号塔CD,信号塔底端C到山脚A的距离AC=13米,在距山脚A水平距离18米的E处,有一高度为10米的建筑物EF,在建筑物顶端F处测得信号塔顶端D的仰角为37°(信号塔及山坡的剖面和建筑物的剖面在同一平面上),则信号塔CD的高度约是( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
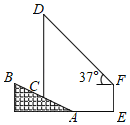
A.22.5米B.27.5米C.32.5米D.45.0米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;
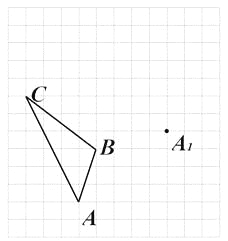
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
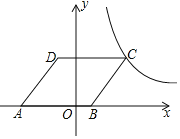
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
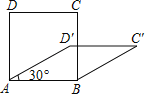
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,

活动类型 | 频数(人数) | 频率 |
运动 | 20 | |
娱乐 | 40 | |
阅读 | ||
其他 | 0.1 |
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
2+22=23﹣2;
2+22+23=24﹣2;
2+22+23+24=25﹣2;
2+22+23+24+25=26﹣2;
…
已知按一定规律排列的一组数:220,221,222,223,224,…,238,239,240,若220=m,则220+221+222+223+224+…+238+239+240=_____(结果用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
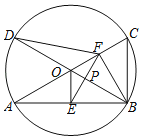
【题目】如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC的中点,连接EF.
(1)设⊙O的半径为1,若∠BAC=30°,求线段EF的长.
(2)连接BF,DF,设OB与EF交于点P,
①求证:PE=PF.
②若DF=EF,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com