
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
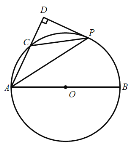
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
【答案】(1)见解析;(2)AP=![]() .
.
【解析】
(1)根据题意连接OP,直接利用切线的定理进行分析证明即可;
(2)根据题意连接BC,交于OP于点G,利用三角函数和勾股定理以及矩形的性质进行综合分析计算即可.
解:(1)证明:连接OP;
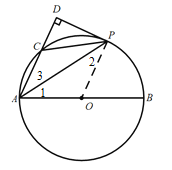
∵OP=OA;
∴∠1=∠2;
又∵P为![]() D的中点;
D的中点;
∴![]()
∴∠1=∠3;
∴∠3=∠2;
∴OP∥DA;
∵∠D=90°;
∴∠OPD=90°;
又∵OP为O半径;
∴DP为O的切线;
(2)连接BC,交于OP于点G;
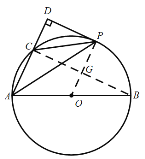
∵AB是圆O的直径;
∴∠ACB为直角;
∵![]()
∴sin∠ABC=![]()
AC=5,则AB=13,半径为![]()
由勾股定理的BC=![]() ,那么CG=6
,那么CG=6
又∵四边形DCGP为矩形;
∴GP=DC=6.5-2.5=4
∴AD=5+4=9;
在Rt△ADP中,AP=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
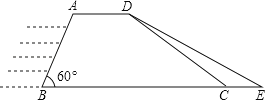
【题目】如图,马边水务部门为加强马边河防汛工作,决定对某水电站水库进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为10![]() 米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
(1)已知需加固的大坝长为120米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角三角形ABC中,∠ACB=90°,BC的垂直平分线交BC点D,交AB于点E,过点A作AF∥CE交直线DE于点F.
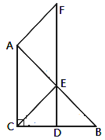
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请证明你的结论;
(3)四边形ACEF有可能是矩形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索.

(1)根据小明的解答(图1)分解因式(a-1)2-8(a-1)+7
(2)根据小丽的思考(图2)解决问题,说明:代数式a2-12a+20的最小值为-16.
(3)求代数式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们知道,若点![]() 将线段
将线段![]() 分成两部分,且
分成两部分,且![]() ,则称点
,则称点![]() 为线段
为线段![]() 的黄金分割点.类似的,我们把有一个内角等于
的黄金分割点.类似的,我们把有一个内角等于![]() 的等腰三角形称为黄金三角形,如图
的等腰三角形称为黄金三角形,如图![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作直线
作直线![]() 分别交直线
分别交直线![]() 和
和![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的度数,并证明
的度数,并证明![]() 是黄金三角形;
是黄金三角形;
(2)求证:点![]() 是线段
是线段![]() 的黄金分割点;
的黄金分割点;
(3)对于实数:![]() ,如果满足
,如果满足![]() ,
,![]()
![]() 则称
则称![]() 为
为![]() ,
,![]() 的黄金数,
的黄金数,![]() 为
为![]() ,
,![]() 的白银数.
的白银数.
①实数![]() ,且
,且![]() 为
为![]() ,1的黄金数,
,1的黄金数,![]() 为
为![]() ,1的白银数,求
,1的白银数,求![]() 的值.
的值.
②实数![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,t的黄金数和白银数,求
,t的黄金数和白银数,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DCE都是等边三角形.
探究发现
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
拓展运用
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
(3)若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.
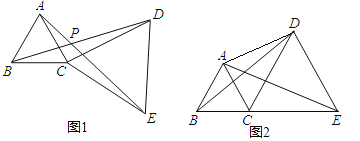
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y=![]() x及y轴所围成的封闭区域内(含边界)的概率是_____.
x及y轴所围成的封闭区域内(含边界)的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为____________(用含a,b的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com