
【题目】如图1,我们知道,若点![]() 将线段
将线段![]() 分成两部分,且
分成两部分,且![]() ,则称点
,则称点![]() 为线段
为线段![]() 的黄金分割点.类似的,我们把有一个内角等于
的黄金分割点.类似的,我们把有一个内角等于![]() 的等腰三角形称为黄金三角形,如图
的等腰三角形称为黄金三角形,如图![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作直线
作直线![]() 分别交直线
分别交直线![]() 和
和![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的度数,并证明
的度数,并证明![]() 是黄金三角形;
是黄金三角形;
(2)求证:点![]() 是线段
是线段![]() 的黄金分割点;
的黄金分割点;
(3)对于实数:![]() ,如果满足
,如果满足![]() ,
,![]()
![]() 则称
则称![]() 为
为![]() ,
,![]() 的黄金数,
的黄金数,![]() 为
为![]() ,
,![]() 的白银数.
的白银数.
①实数![]() ,且
,且![]() 为
为![]() ,1的黄金数,
,1的黄金数,![]() 为
为![]() ,1的白银数,求
,1的白银数,求![]() 的值.
的值.
②实数![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,t的黄金数和白银数,求
,t的黄金数和白银数,求![]() 的值.
的值.

【答案】(1)![]() ,
,![]() 是黄金三角形证明见解析;(2)证明见解析;(3)①
是黄金三角形证明见解析;(2)证明见解析;(3)①![]() ;②
;②![]() 或
或![]()
【解析】
(1)由题意,根据同圆半径相等和三角形内角和,可求![]() 的度数,再由黄金三角形定义可证明
的度数,再由黄金三角形定义可证明![]() 是黄金三角形;
是黄金三角形;
(2)由(1)条件证明![]() ,再由黄金分割定义问题可证明;
,再由黄金分割定义问题可证明;
(3)①根据黄金数和白银数的定义,分别求出对应的a、b的值,则问题可解;
②根据k的正负取值,根据定义分别用k表示m、n,再求出比值即可.
(1)![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,
,
![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
又![]()
![]()
![]()
![]() .
.
则![]()
![]()
![]()
又![]()
![]() 是黄金三角形.
是黄金三角形.
(2)由(1)得,![]()
![]()
![]()
![]()
![]() ,
,
又![]()
![]()
![]() 点
点![]() 是线段
是线段![]() 的黄金分割点.
的黄金分割点.
(3)①![]() 为
为![]() 的黄金数,且实数
的黄金数,且实数![]()
![]()
![]()
![]() (舍),
(舍),![]()
![]() 为
为![]() 的白银数,且实数
的白银数,且实数![]()
![]()
![]()
![]() (舍)
(舍)![]()
②![]() 分别为
分别为![]() 的黄金数和白银数,实数
的黄金数和白银数,实数![]()
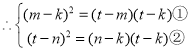
分两种情况:i)当![]() 时,
时,![]()
由①得:![]()
![]()
![]()
由②得:![]()
![]()
![]()
![]()
![]()
ii)当![]() 时,
时,![]() ,由①得:
,由①得:
![]()
![]()
![]()
由②得:![]()
![]()
![]()
![]()
![]()
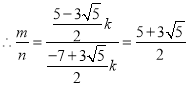
综上, ![]() 的值是
的值是![]() 或
或![]()


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
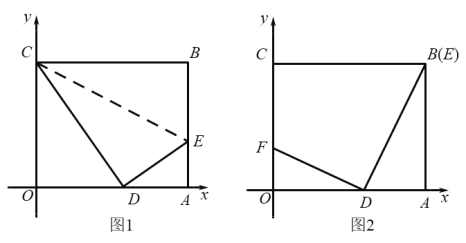
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,矩形OABC的顶点O为原点,AB=8,BC=10,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在边上的点D处,
(1)求AE的长;
(2)如图2,将∠CDE绕着点D逆时针旋转一定的角度,使角的一边DE刚好经过点B,另一边与y轴交于点F,求点F的坐标;
(3)在(2)的条件下,在平面内是否存在一点P,使以点C、D、F、P为顶点的四边形是平行四边形.若存在,直接写出点P的坐标;若不存在,请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元.
(1)销售该运动服每件的利润是多少元;(用含![]() 的式子表示)
的式子表示)
(2)求月销量![]() 与售价
与售价![]() 的关系式;
的关系式;
(3)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的![]() 中,按以下步骤:(1)分别以
中,按以下步骤:(1)分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交
的长为半径作弧,两弧相交![]() 、
、![]() ;(2)作直线
;(2)作直线![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,若
,若![]() ,
,![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
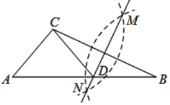
A.直线![]() 是线段
是线段![]() 的垂直平分线B.点
的垂直平分线B.点![]() 为
为![]() 的外心
的外心
C.![]() D.点
D.点![]() 为
为![]() 的内心
的内心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
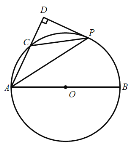
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
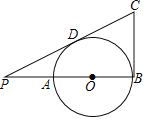
A.1.5B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
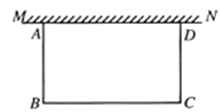
【题目】如图,在足够大的空地上有一段长为![]() 的旧墙
的旧墙![]() ,某人利用旧墙和木栏围成一个矩形菜园
,某人利用旧墙和木栏围成一个矩形菜园![]() ,其中
,其中![]() ,已知矩形菜园的一边靠墙,另三边一共用了
,已知矩形菜园的一边靠墙,另三边一共用了![]() 的木栏.
的木栏.
(1)若![]() ,所围成的矩形菜园的面积为
,所围成的矩形菜园的面积为![]() ,求所利用的旧墙
,求所利用的旧墙![]() 的长;
的长;
(2)求矩形菜园![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,![]() ,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接
,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接![]() ,图中阴影部分的面积是( )
,图中阴影部分的面积是( )
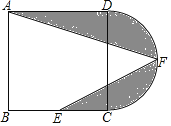
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com