
【题目】发现与探索.

(1)根据小明的解答(图1)分解因式(a-1)2-8(a-1)+7
(2)根据小丽的思考(图2)解决问题,说明:代数式a2-12a+20的最小值为-16.
(3)求代数式-a2+12a-8的最大值.
【答案】(1)![]() ;(2)说明见解析;(3)最大值为28.
;(2)说明见解析;(3)最大值为28.
【解析】
(1)先配成完全平方式与一个平方数差的形式,再运用平方差公式进行因式分解即可;
(2)依据小丽的思路通过配方进行证明即可;
(3)原式先提取“-”,再通过配方,得-(a-6)2+28,根据-(a-6)2≤0可得解
(1)(a-1)2-8(a-1)+7
=(a-1)2-8(a-1)+16-16+7
=(a-5)2-32
=(a-8)(a-2);
(2)a2-12a+20
=a2-12a+36-36+20
=(a-6)2-16
∵无论a取何值(a-6)2≥0
∴代数式(a-6)2-16≥-16,
∴a2-12a+20的最小值为-16;
(3)-a2+12a-8.
=-(a2-12a+8)
=-(a2-12a+36-36+8)
=-(a-6)2+36-8
=-(a-6)2+28
∵a取何值-(a-6)2≤0,
∴代数式-(a-6)2+28≤28
∴-a2+12a-8的最大值为28.


科目:初中数学 来源: 题型:
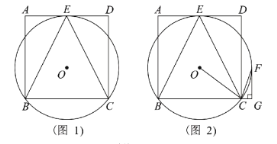
【题目】已知正方形![]() ,
,![]() 经过点
经过点![]() ,
,![]() ,且与
,且与![]() 边相切于点
边相切于点![]() ,连接
,连接![]() .
.
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,点
,点![]() 是圆
是圆![]() 上一点
上一点![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①求证:![]() 是
是![]() 的切线;
的切线;
②若正方形![]() 的边长为
的边长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
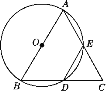
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
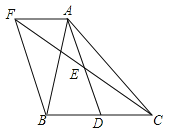
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() 是
是![]() 的中点,过
的中点,过![]() 点作
点作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)如果![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元.
(1)销售该运动服每件的利润是多少元;(用含![]() 的式子表示)
的式子表示)
(2)求月销量![]() 与售价
与售价![]() 的关系式;
的关系式;
(3)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,这一天世界各地都会举办诸多与阅读有关的活动.某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
个世界读书日,这一天世界各地都会举办诸多与阅读有关的活动.某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
“读书节”活动计划书 | ||
书本类别 |
|
|
进价(单位:元) | 18 | 12 |
备注 | 用不超过16800元购进
| |
(1)陈经理查看计划书发现:![]() 类图书的标价是
类图书的标价是![]() 类图书标价的
类图书标价的![]() 倍,若顾客用
倍,若顾客用![]() 元购买图书,能单独购买
元购买图书,能单独购买![]() 类图书的数量恰好比单独购买
类图书的数量恰好比单独购买![]() 类图书的数量少
类图书的数量少![]() 本.请求出
本.请求出![]() 、
、![]() 两类图书的标价.
两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案:![]() 类图书每本按标价降价
类图书每本按标价降价![]() 元
元![]() 销售,
销售, ![]() 类图书价格不变.那么书店应如何进货才能获得最大利润?
类图书价格不变.那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
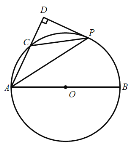
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
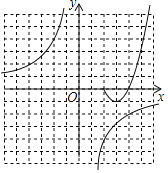
【题目】某数学小组对函数y1=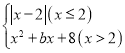 图象和性质进行探究.当x=4时,y1=0.
图象和性质进行探究.当x=4时,y1=0.
(1)当x=5时,求y1的值;
(2)在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;
(3)进一步探究函数图象并解决问题:已知函数y2=﹣![]() 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
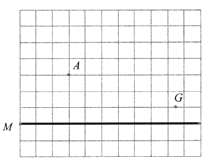
【题目】如图,在每个小正方形的边长为1的网格中,A,M,N均在格点上.在线段![]() 上有一动点B,以
上有一动点B,以![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一个小正方形边的中点.
,G是一个小正方形边的中点.
(1)当点B的位置满足![]() 时,求此时
时,求此时![]() 的长_______;
的长_______;
(2)请用无刻度的直尺,在如图所示的网格中,画出一个点C,使其满足线段![]() 最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com